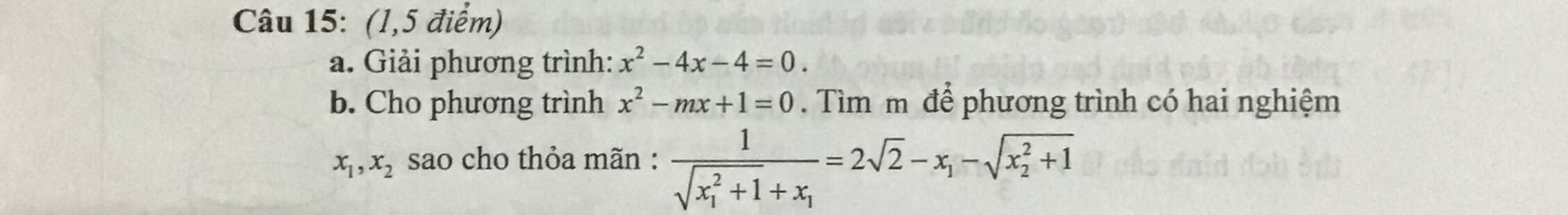\(x^2-mx+1=0\)
phương trình có nghiệm \(\Leftrightarrow\Delta=m^2-4\ge0\Leftrightarrow\left[{}\begin{matrix}m\le-2\\m\ge2\end{matrix}\right.\)
Theo Viéte : \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=1\end{matrix}\right.\)
Ta có : \(\dfrac{1}{\sqrt{x_1^2+1}+x_1}=2\sqrt{2}-x_1-\sqrt{x_2^2+1}\)
\(\Leftrightarrow\dfrac{\sqrt{x_1^2+1}-x_1}{x_1^2+1-x_1^2}=2\sqrt{2}-x_1-\sqrt{x_2^2+1}\)
\(\Leftrightarrow\sqrt{x_1^2+1}-x_1=2\sqrt{2}-x_1-\sqrt{x_2^2+1}\)
\(\Leftrightarrow\sqrt{x_1^2+1}+\sqrt{x_2^2+1}=2\sqrt{2}\)
Mà \(x^2-mx+1=0\left(gt\right)\Rightarrow mx-1=x^2\)
\(\Rightarrow\sqrt{mx_1-1+1}+\sqrt{mx_2-1+1}=2\sqrt{2}\)
\(\Leftrightarrow\left(\sqrt{mx_1}+\sqrt{mx_2}\right)^2=8\)
\(\Leftrightarrow mx_1+2\sqrt{m^2x_1x_2}+mx_2=8\)
\(\Leftrightarrow m\left(x_1+x_2\right)+2\sqrt{m^2}=8\)
\(m^2+2m=8\Leftrightarrow\left[{}\begin{matrix}m=2\left(n\right)\\m=-4\left(n\right)\end{matrix}\right.\)
Vậy m = 2 hoặc m = -4 thì thỏa ycbt