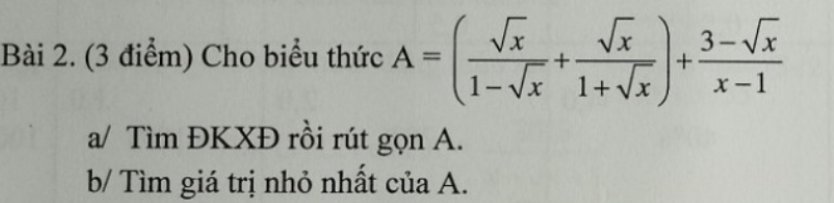a.
ĐKXĐ: \(x\ne0;y\ne-1\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2x-1}{x}+\dfrac{y-1}{y+1}=3\\\dfrac{2x-1}{2x}+\dfrac{3\left(y-1\right)}{y+1}=2\end{matrix}\right.\)
Đặt \(\left\{{}\begin{matrix}\dfrac{2x-1}{x}=u\\\dfrac{y-1}{y+1}=v\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}u+v=3\\\dfrac{u}{2}+3v=2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}u+v=3\\u+6v=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u=3-v\\5v=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}u=3-v\\v=\dfrac{1}{5}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u=\dfrac{14}{5}\\v=\dfrac{1}{5}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{2x-1}{x}=\dfrac{14}{5}\\\dfrac{y-1}{y+1}=\dfrac{1}{5}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}5\left(2x-1\right)=14x\\5\left(y-1\right)=y+1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{5}{4}\\y=\dfrac{3}{2}\end{matrix}\right.\)
b.
ĐKXĐ: \(x\ne-1;y\ne-2\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x+1}-\dfrac{3}{y+2}=0\\\dfrac{2\left(x+1\right)+2}{x+1}+\dfrac{5\left(y+2\right)-12}{y+2}=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x+1}-\dfrac{3}{y+2}=0\\2+\dfrac{2}{x+1}+5-\dfrac{12}{y+2}=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x+1}-\dfrac{3}{y+2}=0\\\dfrac{2}{x+y}-\dfrac{12}{y+2}=-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x+1}=\dfrac{3}{y+2}\\\dfrac{3}{y+2}-\dfrac{12}{y+2}=-3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x+1}{2}=\dfrac{y+2}{3}\\\dfrac{-9}{y+2}=-3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{2\left(y+2\right)}{3}-1\\y+2=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)

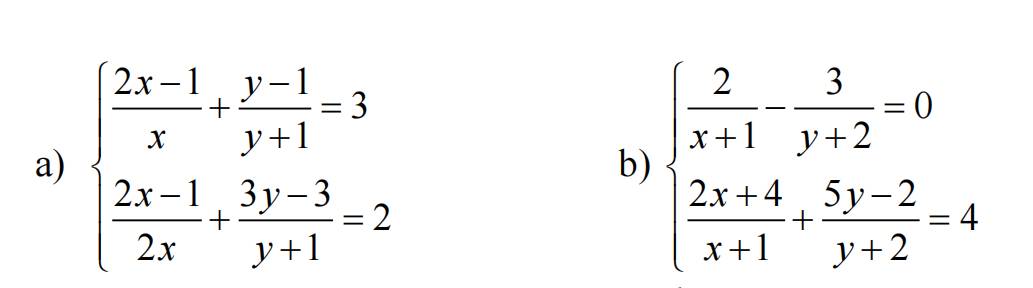













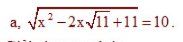




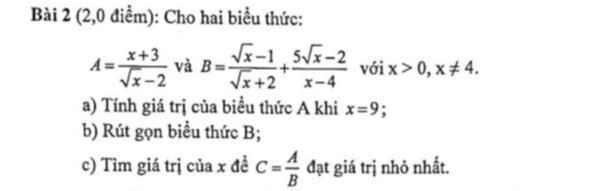 mn giúp mik câu c vs ạ
mn giúp mik câu c vs ạ