a: Xét (O) có
MD,MA là các tiếp tuyến
Do đó: MD=MA và MO là phân giác của góc DMA
Xét (O') có
MA,ME là các tiếp tuyến
Do đó: MA=ME và MO' là phân giác của góc AME
Ta có: MD=MA
MA=ME
Do đó: MD=ME
=>M là trung điểm của DE
=>DE=2DM
mà DM=MA
nên DE=2MA
Ta có; MO là phân giác của góc DMA
=>\(\hat{DMA}=2\cdot\hat{OMA}\)
MO' là phân giác của góc AME
=>\(\hat{AME}=2\cdot\hat{AMO^{\prime}}\)
Ta có: \(\hat{DMA}+\hat{EMA}=180^0\) (hai góc kề bù)
=>\(2\left(\hat{OMA}+\hat{O^{\prime}MA}\right)=180^0\)
=>\(2\cdot\hat{O^{\prime}MO}=180^0\)
=>\(\hat{O^{\prime}MO}=90^0\)
b: Xét ΔMO'O vuông tại M có MA là đường cao
nên \(MA^2=OA\cdot O^{\prime}A=6\cdot2=12\)
=>\(MA=2\sqrt3\left(\operatorname{cm}\right)\)
Xét ΔMAO vuông tại A có tan MOA\(=\frac{MA}{AO}=\frac{2\sqrt3}{6}=\frac{\sqrt3}{3}\)
nên \(\hat{MOA}=30^0\)
Xét (O) có
MD,MA là các tiếp tuyến
Do đó: OM là phân giác của góc AOD
=>\(\hat{AOD}=2\cdot\hat{AOM}=2\cdot30^0=60^0\)
c: Xét ΔDAE có
AM là đường trung tuyến
\(AM=\frac{DE}{2}\)
Do đó: ΔDAE vuông tại A
=>DA⊥EA
Xét (O) có
ΔDAF nội tiếp
DF là đường kính
Do đó: ΔDAF vuông tại A
=>DA⊥AF
Ta có: DA⊥AF
DA⊥ AE
mà AF,AE có điểm chung là A
nên A,F,E thẳng hàng
d: Xét (O) có
ΔBDA nội tiếp
BA là đường kính
Do đó: ΔBDA vuông tại D
=>AD⊥BK tại D
Xét (O') có
ΔAEC nội tiếp
AC là đường kính
Do đó: ΔAEC vuông tại E
=>AE⊥KC tại E
Xét tứ giác KDAE có \(\hat{KDA}=\hat{KEA}=\hat{DAE}=90^0\)
nên KDAE là hình chữ nhật
=>KA cắt DE tại trung điểm của mỗi đường
mà M là trung điểm của DE
nên M là trung điểm của KA
=>K,M,A thẳng hàng
e: Xét ΔKAB vuông tại A có AD là đường cao
nên \(KD\cdot KB=KA^2\)
mà KA=DE(ADKE là hình chữ nhật)
nên \(KD\cdot KB=DE^2\)
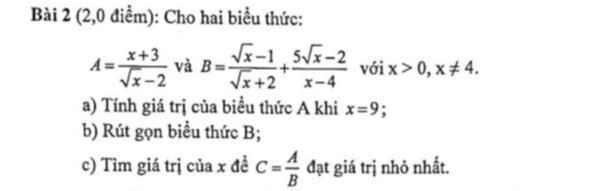mn giúp mik câu c vs ạ
