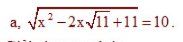`a,` ĐKXĐ: `x>=0;x\ne1`
`A=...=(sqrtx(1+sqrtx)+sqrtx(1-sqrtx)+sqrtx-3)/((1-sqrtx)(1+sqrtx))`
`=(sqrtx+x+sqrtx-x+sqrtx-3)/((1-sqrtx)(1+sqrtx))`
`=(3sqrtx-3)/((1-sqrtx)(1+sqrtx))`
`=-3/(1+sqrtx)`
`b,A=-3/(1+sqrtx)`
Vì `x>=0` nên `1+sqrtx>=1` nên `3/(1+sqrtx)<=3` suy ra `A>=-3`
Dấu "=" xảy ra `<=>x=0`
Vậy `A_(min)=-3<=>x=0`
`a)->` ĐKXĐ : `x>=0;x\ne1`
`b)` Ta có :
`A=((\sqrtx)/(1-\sqrtx)+(\sqrtx)/(1+\sqrtx))+(3-\sqrtx)/(x-1)`
`A=[(\sqrtx(1+\sqrtx)+\sqrtx(1-\sqrtx))/(1-x)]+(3-\sqrtx)/(x-1)`
`A=[(\sqrtx+x+\sqrtx-x)/(1-x)]+(3-\sqrtx)/(x-1)`
`A=(2\sqrtx)/(1-x)+(3-\sqrtx)/(x-1)`
`A=(3-\sqrtx)/(x-1)-(2\sqrtx)/(x-1)`
`A=(3+\sqrtx)/(x-1)`
Vậy `A=(3+\sqrtx)/(x-1)` khi `x>=0;x\ne1`


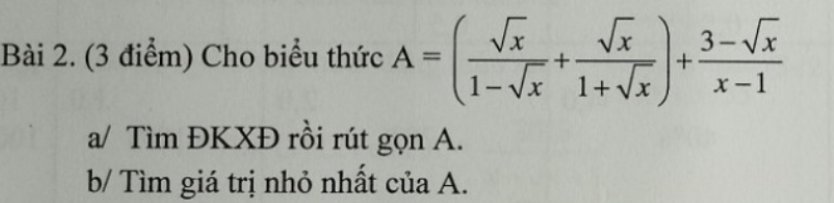










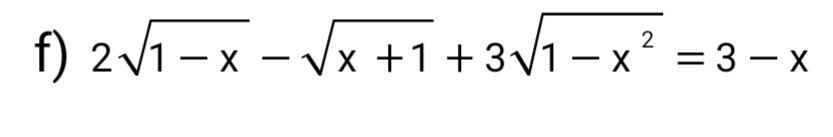 Giải pt . Mn giúp mik vs
Giải pt . Mn giúp mik vs

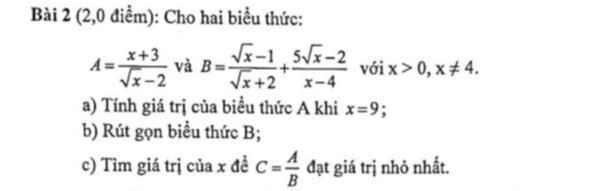 mn giúp mik câu c vs ạ
mn giúp mik câu c vs ạ