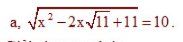\(\sqrt{x^2-2x\sqrt{11}+11}=10\)
\(< =>\sqrt{\left(x-\sqrt{11}\right)^2}=10\\ < =>\left|x-\sqrt{11}\right|=10\\ < =>\left[{}\begin{matrix}x-\sqrt{11}=10\\x-\sqrt{11}=-10\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=10+\sqrt{11}\\x=-10+\sqrt{11}\end{matrix}\right.\)
\(1-\sqrt{1+5x}=x\left(đk:x\ge-\dfrac{1}{5}\right)\\ < =>\sqrt{1+5x}=1-x\\ < =>\left\{{}\begin{matrix}1-x\ge0\\1+5x=1-2x+x^2\end{matrix}\right.\\ < =>\left\{{}\begin{matrix}x\le1\\x^2-7x=0\end{matrix}\right.\\ < =>\left\{{}\begin{matrix}x\le1\\x\left(x-7\right)=0\end{matrix}\right.\\ < =>\left\{{}\begin{matrix}x\le1\\\left[{}\begin{matrix}x=0\left(tm\right)\\x=7\left(ktm\right)\end{matrix}\right.\end{matrix}\right.\\ < =>x=0\)