\(\Delta=\left(2m+3\right)^2+4\left(2m+4\right)=4m^2+20m+25=\left(2m+5\right)^2\ge0;\forall m\)
Pt đã cho luôn có 2 nghiệm với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m-3\\x_1x_2=-2m-4\end{matrix}\right.\)
\(\left|x_1\right|+\left|x_2\right|=5\Leftrightarrow x_1^2+x_2^2+2\left|x_1x_2\right|=25\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2+2\left|x_1x_2\right|=25\)
\(\Leftrightarrow\left(2m-3\right)^2+2\left(2m+4\right)+2\left|2m+4\right|=25\)
\(\Leftrightarrow4m^2-8m-8+4\left|m+2\right|=0\)
TH1: \(m\ge-2\)
\(\Rightarrow4m^2-8m-8+4\left(m+2\right)=0\)
\(\Leftrightarrow4m^2-4m=0\Rightarrow\left[{}\begin{matrix}m=0\\m=1\end{matrix}\right.\) (thỏa mãn)
TH2: \(m\le-2\)
\(\Rightarrow4m^2-8m-8-4\left(m+2\right)=0\)
\(\Leftrightarrow4m^2-12m-16=0\Rightarrow\left[{}\begin{matrix}m=-1\left(loại\right)\\m=4\left(loại\right)\end{matrix}\right.\)


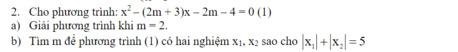

















 vẽ hình vs làm câu a) . b) thôi ạ, e cần gấp lắm á
vẽ hình vs làm câu a) . b) thôi ạ, e cần gấp lắm á

