Câu 1:
a: \(A=\dfrac{\sqrt{x}+1}{\sqrt{x}}+\dfrac{2}{1-\sqrt{x}}+\dfrac{3\sqrt{x}+1}{x-\sqrt{x}}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}}-\dfrac{2}{\sqrt{x}-1}+\dfrac{3\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)-2\sqrt{x}+3\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x-1+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\cdot\sqrt{x}}=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
b: A>1/2
=>A-1/2>0
=>\(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{1}{2}>0\)
=>\(\dfrac{2\left(\sqrt{x}+1\right)-\sqrt{x}+1}{2\left(\sqrt{x}-1\right)}>0\)
=>\(\dfrac{2\sqrt{x}+2-\sqrt{x}+1}{2\left(\sqrt{x}-1\right)}>0\)
=>\(\dfrac{\sqrt{x}+3}{2}\cdot\dfrac{1}{\sqrt{x}-1}>0\)
=>\(\sqrt{x}-1>0\)
=>x>1
1.
a)\(A=\dfrac{\sqrt{x}+1}{\sqrt{x}}+\dfrac{2}{1-\sqrt{x}}+\dfrac{3\sqrt{x}+1}{x-\sqrt{x}}\left(x>0,x\ne1\right)\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}}+\dfrac{2}{1-\sqrt{x}}+\dfrac{3\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{2\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}+\dfrac{3\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x-1-2\sqrt{x}+3\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\) (đpcm)
b) \(A>\dfrac{1}{2}\Leftrightarrow\dfrac{\sqrt{x}+1}{\sqrt{x}-1}>\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{1}{2}>0\)
\(\Leftrightarrow\dfrac{2\sqrt{x}+2-\sqrt{x}+1}{2\left(\sqrt{x}-1\right)}>0\)
\(\Leftrightarrow\dfrac{\sqrt{x}+3}{2\left(\sqrt{x}-1\right)}>0\)
\(\Leftrightarrow\sqrt{x}-1>0\Leftrightarrow x>1\)
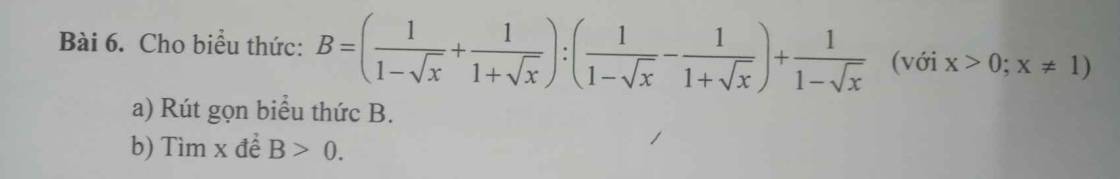Câu (a) đã rút gọn được là 
làm cho mình câu đầu để làm mẫu mấy câu sau hihi