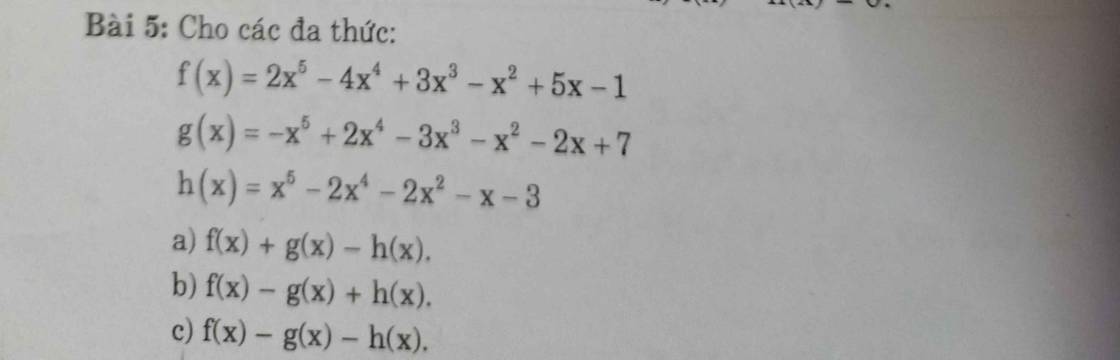Bài 1
a) \(7x=3y\Rightarrow\dfrac{x}{3}=\dfrac{y}{7}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{3}=\dfrac{y}{7}=\dfrac{x-y}{3-7}=\dfrac{16}{-4}=-4\)
\(\dfrac{x}{3}=-4\Rightarrow x=-4.3=-12\)
\(\dfrac{y}{7}=-4\Rightarrow y=-4.7=-28\)
Vậy \(x=-12;y=-28\)
b) \(4x=5y\Rightarrow\dfrac{x}{5}=\dfrac{y}{4}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{5}=\dfrac{y}{4}=\dfrac{x+y}{5+4}=\dfrac{27}{9}=3\)
\(\dfrac{x}{5}=3\Rightarrow x=3.5=15\)
\(\dfrac{y}{4}=3\Rightarrow y=3.4=12\)
Vậy \(x=15;y=12\)
Bài 2
a) \(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}\Rightarrow\dfrac{a}{2}=\dfrac{2b}{6}=\dfrac{3c}{12}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{a}{2}=\dfrac{2b}{6}=\dfrac{3c}{12}=\dfrac{a+2b-3c}{2+6-12}=\dfrac{-20}{-4}=5\)
\(\dfrac{a}{2}=5\Rightarrow a=5.2=10\)
\(\dfrac{b}{3}=5\Rightarrow b=5.3=15\)
\(\dfrac{c}{4}=5\Rightarrow c=5.4=20\)
Vậy \(a=10;b=15;c=20\)
b) \(3a=5b\Rightarrow\dfrac{a}{5}=\dfrac{b}{3}\Rightarrow\dfrac{a}{10}=\dfrac{b}{6}\left(1\right)\)
\(7b=2c\Rightarrow\dfrac{b}{2}=\dfrac{c}{7}\Rightarrow\dfrac{b}{6}=\dfrac{c}{21}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\dfrac{a}{10}=\dfrac{b}{6}=\dfrac{c}{21}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{a}{10}=\dfrac{b}{6}=\dfrac{c}{21}=\dfrac{a+b+c}{10+6+21}=\dfrac{74}{37}=2\)
\(\dfrac{a}{10}=2\Rightarrow a=2.10=20\)
\(\dfrac{b}{6}=2\Rightarrow b=2.6=12\)
\(\dfrac{c}{21}=2\Rightarrow c=2.21=42\)
Vậy \(a=20;b=12;c=42\)
Bài 3
Gọi \(x\) (người), \(y\) (người), \(z\) (người) lần lượt là số công nhân của nhóm thứ nhất, nhóm thứ hai và nhóm thứ ba \(\left(x,y,z\in Z^+\right)\)
Do ba nhóm xây ba phân xưởng như nhau và năng suất của mỗi công nhân là như nhau nên số công nhân và số ngày hoàn thành là hai đại lượng tỉ lệ nghịch
\(\Rightarrow40x=60y=50z\)
\(\Rightarrow\dfrac{40x}{600}=\dfrac{60y}{600}=\dfrac{50z}{600}\)
\(\Rightarrow\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{12}\)
Áp dụng tính chất của dảy tỉ số bằng nhau, ta có:
\(\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{12}=\dfrac{x-y}{15-10}=\dfrac{3}{3}=1\)
\(\dfrac{x}{15}=1\Rightarrow x=15\)
\(\dfrac{y}{10}=1\Rightarrow y=10\)
\(\dfrac{z}{12}=1\Rightarrow z=12\)
Vậy số công nhân của nhóm thứ nhất, nhóm thứ hai và nhóm thứ ba lần lượt là: 15 người, 10 người và 12 người
Bài 4
Gọi \(x\) (giờ) là số giờ đào xong con mương khi tăng thêm 10 người \(\left(x>0\right)\)
Do cùng đào một con mương và năng suất của mỗi người là như nhau nên số người và số giờ đào xong con mương là hai đại lượng tỉ lệ nghịch
\(\Rightarrow x.\left(30+10\right)=30.8\)
\(40x=240\)
\(x=\dfrac{240}{40}\)
\(x=6\) (nhận)
Thời gian giảm đi:
\(8-6=2\) (giờ)
Bài 5
\(30\) phút \(=0,5\) giờ
Gọi \(x\) (giờ) là thời gian xe thứ nhất đi hết quãng đường AB \(\left(x>0\right)\)
Thời gian xe thứ hai đi hết quãng đường AB là: \(x+0,5\) (giờ)
Do cùng đi một quãng đường AB nên:
\(80x=60\left(x+0,5\right)\)
\(80x=60x+30\)
\(80x-60x=30\)
\(20x=30\)
\(x=\dfrac{30}{20}\)
\(x=1,5\) (nhận)
Thời gian xe thứ nhất đi hết quãng đường AB là 1,5 giờ, thời gian xe thứ hai đi hết quãng đường AB là \(1,5+0,5=2\) giờ
Quãng đường AB dài:
\(60.2=120km\)
Bài 8
a) \(\dfrac{1}{4}x^3\left(2x^2+4x^3-6x-7\right)\)
\(=\dfrac{1}{4}x^3.2x^2+\dfrac{1}{4}x^3.4x^3+\dfrac{1}{4}x^3.\left(-6x\right)+\dfrac{1}{4}x^3.\left(-7\right)\)
\(=\dfrac{1}{2}x^5+x^6-\dfrac{3}{2}x^4-\dfrac{7}{4}x^3\)
\(=x^6+\dfrac{1}{2}x^5-\dfrac{3}{2}x^4-\dfrac{7}{4}x^3\)
b) \(\left(2x-1\right)\left(4x^3-7\right)\)
\(=2x.\left(4x^3-7\right)-1.\left(4x^3-7\right)\)
\(=2x.4x^3+2x.\left(-7\right)-4x^3+7\)
\(=8x^4-14x-4x^3+7\)
\(=8x^4-4x^3-14x+7\)
c) \(\left(3x-1\right)\left(3x+5\right)-7\left(x^2+2\right)\)
\(=3x.\left(3x+5\right)-1.\left(3x+5\right)+\left(-7\right).x^2+\left(-7\right).2\)
\(=3x.3x+3x.5-3x-5-7x^2-14\)
\(=9x^2+15x-3x-5-7x^2-14\)
\(=2x^2+12x-19\)
d) \(\left(5x^6-2x^5+\dfrac{1}{3}x^4\right):\left(\dfrac{1}{2}x^3\right)\)
\(=\left(5x^6\right):\left(\dfrac{1}{2}x^3\right)+\left(-2x^5\right):\left(\dfrac{1}{2}x^3\right)+\left(\dfrac{1}{3}x^4\right):\left(\dfrac{1}{2}x^3\right)\)
\(=10x^3-4x^2+\dfrac{2}{3}x\)
e) \(\left(x^3+x^2-x+1\right):\left(x+2\right)\)
\(=\left(x^3+2x^2-x^2-2x+x+2-1\right):\left(x+2\right)\)
\(=\left[\left(x^3+2x^2\right)-\left(x^2+2x\right)+\left(x+2\right)-1\right]:\left(x+2\right)\)
\(=\left[x^2\left(x+2\right)-x\left(x+2\right)+\left(x+2\right)-1\right]:\left(x+2\right)\)
\(=\left[\left(x+2\right)\left(x^2-x+1\right)-1\right]:\left(x+2\right)\)
\(=\left(x+2\right)\left(x^2-x+2\right):\left(x+2\right)-1:\left(x+2\right)\)
\(=x^2-x+1-\dfrac{1}{x+2}\)
Bài 9
Số chấm xuất hiện của con xúc xắc có thể là: \(1;2;3;4;5;6\)
a) "Số chấm xuất hiện lớn hơn 1" là biến cố ngẫu nhiên vì có thể xuất hiện 1 chấm
b) "Số chấm xuất hiện trong nhỏ hơn 5" là biến cố ngẫu nhiên vì có thể xuất hiện 5 chấm, 6 chấm
c) "Số chấm xuất hiện là số lẻ" là biến cố ngẫu nhiên vì có thể xuất hiện 2 chấm, 4 chấm, 6 chấm
mn ơi giúp em, nhanh ạ, chỉ cần làm đến bài 2 thôi,bài 1 chỉ cần làm đến câu 17
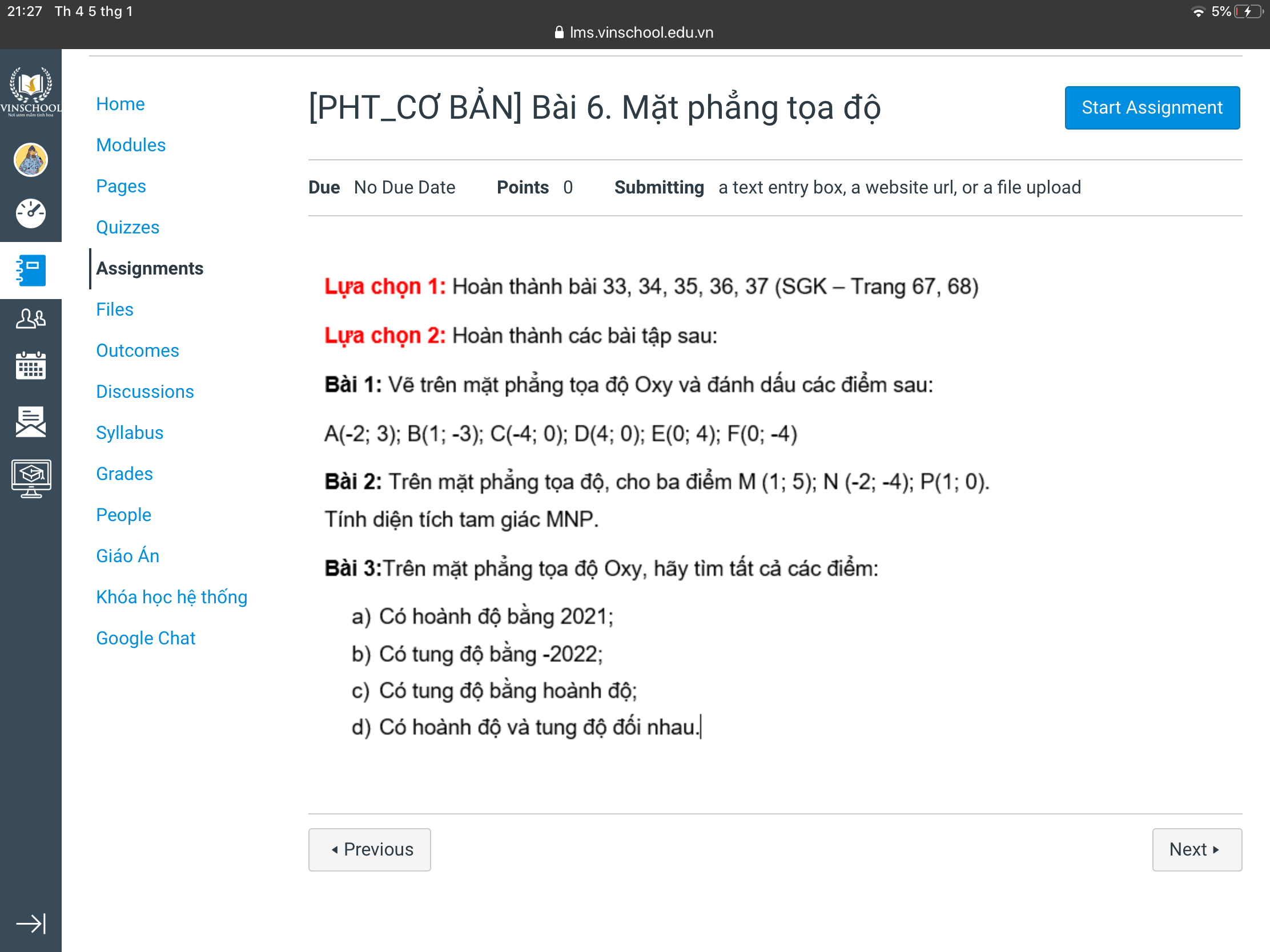Làm giúp e câu 3 với ạ🥺
