a: Xét tứ giác ABOC có
\(\widehat{ABO}+\widehat{ACO}=180^0\)
Do đó: ABOC là tứ giác nội tiếp(1)
Xét tứ giác OHAC có \(\widehat{OHA}+\widehat{OCA}=180^0\)
nên OHAC là tứ giác nội tiếp(2)
Từ (1) và (2) suy ra A,B,C,H,O cùng thuộc 1 đường tròn
b: \(\widehat{BHA}=\widehat{BOA}\)
\(\widehat{AHC}=\widehat{COA}\)
mà \(\widehat{BOA}=\widehat{COA}\)
nên \(\widehat{BHA}=\widehat{CHA}\)
hay HA là tia phân giác của góc BHC














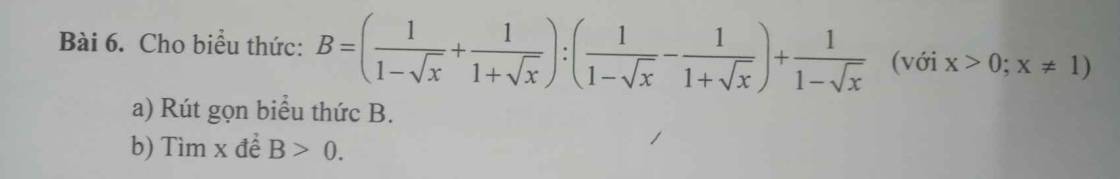 Câu (a) đã rút gọn được là
Câu (a) đã rút gọn được là 


 Ai giúp em với ạ em cần rất gấp bài 4 thôi ạ
Ai giúp em với ạ em cần rất gấp bài 4 thôi ạ
