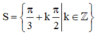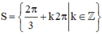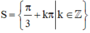\(\Leftrightarrow\dfrac{1}{2}\sin2x+\dfrac{\sqrt{3}}{2}\cos2x=\dfrac{-\sqrt{3}}{2}\)
\(\Leftrightarrow\sin2x\cdot\cos\dfrac{\pi}{3}+\cos2x\cdot\sin\dfrac{\pi}{3}=\dfrac{-\sqrt{3}}{2}\)
\(\Leftrightarrow\sin\left(2x+\dfrac{\pi}{3}\right)=\dfrac{-\sqrt{3}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+\dfrac{\pi}{3}=-\dfrac{\pi}{3}+k2\pi\\2x+\dfrac{\pi}{3}=\pi+\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{2\pi}{3}+k2\pi\\2x=\pi+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k\pi\\x=\dfrac{\pi}{2}+k\pi\end{matrix}\right.\left(k\in Z\right)\)
`sin 2x+\sqrt{3} cos 2x=-\sqrt{3}`
`<=>1/2 sin 2x+\sqrt{3}/2 cos 2x=-\sqrt{3}/2`
`<=>sin``\pi /6 sin 2x+ cos``\pi/6 cos 2x=-\sqrt{3}/2`
`<=>cos (\pi/6 - 2x)=-\sqrt{3}/2`
`<=>` $\left[\begin{matrix} \dfrac{\pi}{6}-2x=\dfrac{5\pi}{6}+k2\pi\\ \dfrac{\pi}{6}-2x=\dfrac{-5\pi}{6}+k2\pi\end{matrix}\right.$ `(k in ZZ)`
`<=>` $\left[\begin{matrix} x=\dfrac{-\pi}{3}-k\pi\\ x=\dfrac{\pi}{2}-k\pi\end{matrix}\right.$ `(k in ZZ)`