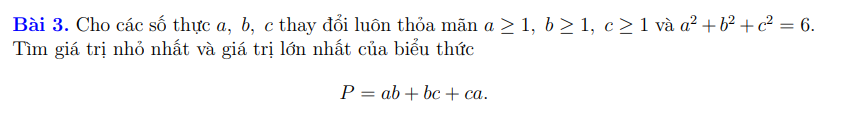Min:
Do \(\left\{{}\begin{matrix}a;b;c\ge1\\a^2+b^2+c^2=6\end{matrix}\right.\) \(\Rightarrow1\le a;b;c\le2\)
\(\Rightarrow\left(a-1\right)\left(a-2\right)\le0\Rightarrow a^2+2\le3a\Rightarrow a\ge\dfrac{a^2+2}{3}\)
Tương tự: \(b\ge\dfrac{b^2+2}{3}\) ; \(c\ge\dfrac{c^2+2}{3}\)
\(\Rightarrow a+b+c\ge\dfrac{a^2+b^2+c^2+6}{3}=4\)
\(\Rightarrow\left(a+b+c\right)^2\ge16\)
\(\Rightarrow6+2\left(ab+bc+ca\right)\ge16\)
\(\Rightarrow ab+bc+ca\ge5\)
\(P_{min}=5\) khi \(\left(a;b;c\right)=\left(1;1;2\right)\) và các hoán vị
Đúng 0
Bình luận (0)
