Câu 3:
a.
Biến đổi biểu thức A ta được:
\(A=\dfrac{x}{1-x}+\dfrac{5}{x}=\dfrac{x^2-5x+5}{x-x^2}\)
Ta có:
\(A-\left(5+2\sqrt{5}\right)=\dfrac{\left[\left(12+4\sqrt{5}\right)x-10-2\sqrt{5}\right]^2}{24+8\sqrt{5}}\ge0\)
Do đó:
\(A_{min}=5+2\sqrt{5}\) khi \(x=\dfrac{5-\sqrt{5}}{4}\)
b.
Từ giả ta có các nhận xét sau
\(\sqrt{2022}=\Sigma\sqrt{a^2+b^2}\ge\Sigma\dfrac{a+b}{\sqrt{2}}=\sqrt{2}\left(a+b+c\right)\)
\(\Rightarrow a+b+c\le\sqrt{1011}\)
\(\sqrt{2022}=\Sigma\sqrt{a^2+b^2}\le\sqrt{3\left[2\left(a^2+b^2+c^2\right)\right]}\)
\(\Rightarrow a^2+b^2+c^2\ge337\)
Do vai trò của a, b, c bình đẳng nên ta có thể giả sử:
\(a\le b\le c\)
\(\Rightarrow\left\{{}\begin{matrix}a^2\le b^2\le c^2\\\dfrac{1}{b+c}\le\dfrac{1}{c+a}\le\dfrac{1}{a+b}\end{matrix}\right.\)
Áp dụng bđt Chebyshev cho hai bộ số cùng chiều
\(\left(a^2,b^2,c^2\right)\) và \(\left(\dfrac{1}{b+c},\dfrac{1}{c+a},\dfrac{1}{a+b}\right)\) :
\(VT\ge\dfrac{1}{3}.\left(a^2+b^2+c^2\right)\left(\dfrac{1}{b+c}+\dfrac{1}{c+a}+\dfrac{1}{a+b}\right)\ge\dfrac{3\left(a^2+b^2+c^2\right)}{2\left(a+b+c\right)}\ge\dfrac{\sqrt{1011}}{2}\)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{\sqrt{1011}}{3}\)
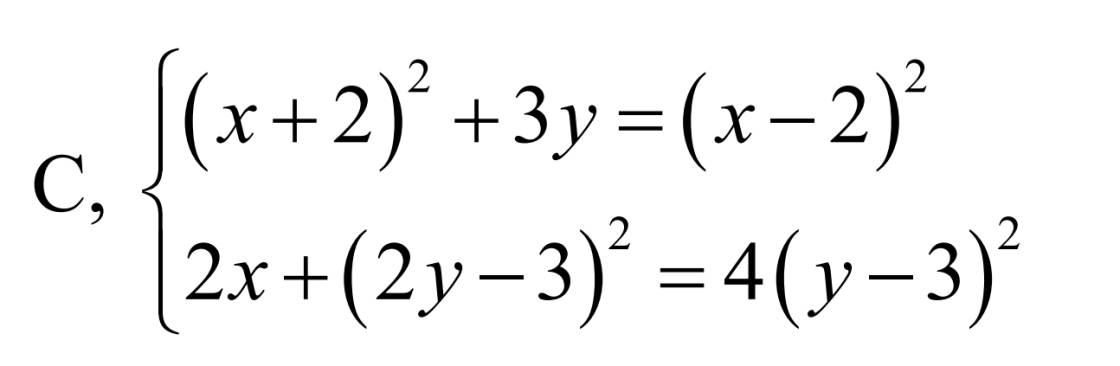
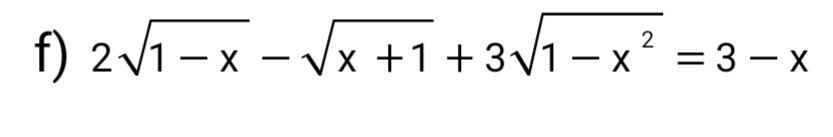Giải pt . Mn giúp mik vs
