\(\left\{{}\begin{matrix}\left(x+2\right)^2+3y=\left(x-2\right)^2\\2x+\left(2y-3\right)^2=4\left(y-3\right)^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x^2+4x+4+3y=x^2-4x+4\\2x+4y^2-12y+9=4y^2-24y+36\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x+3y+4=-4x+4\\2x-12y+9=-24y+36\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}8x+3y=0\\2x+12y=27\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}8x+3y=0\\8x+48y=108\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-45y=-108\\8x+3y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=2,4\\x=-\dfrac{3}{8}y=-0,9\end{matrix}\right.\)

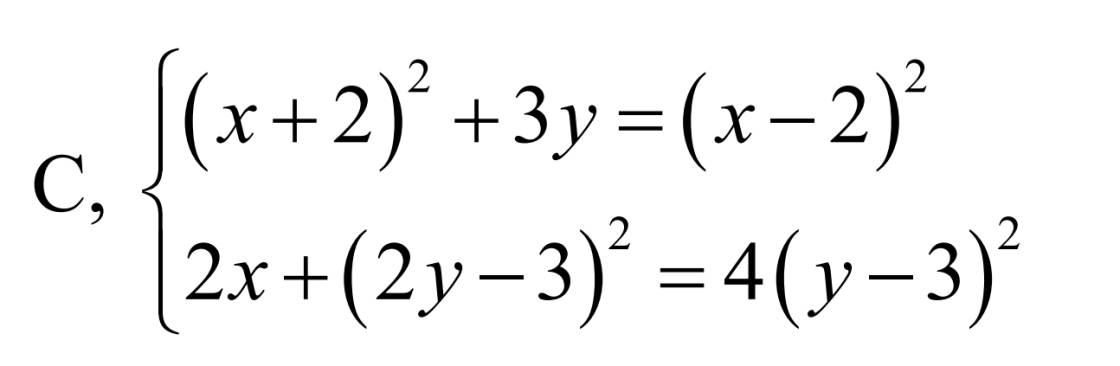












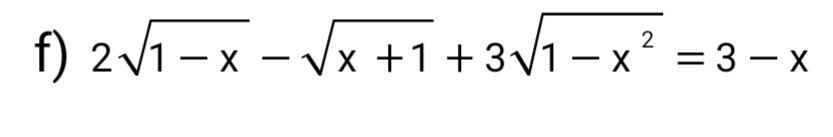 Giải pt . Mn giúp mik vs
Giải pt . Mn giúp mik vs

