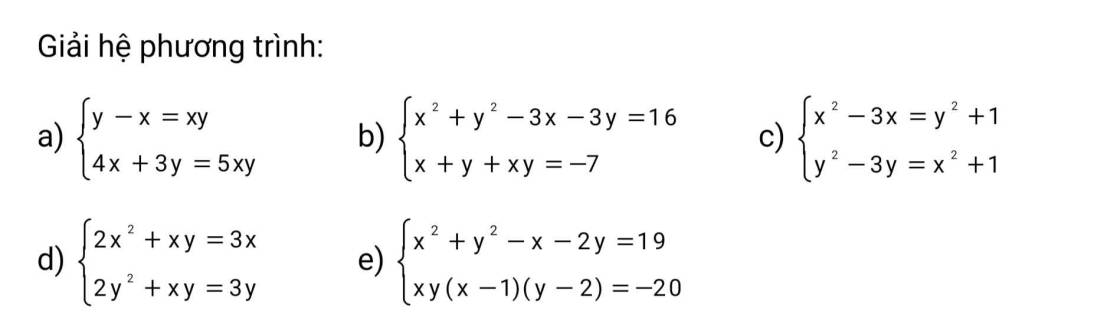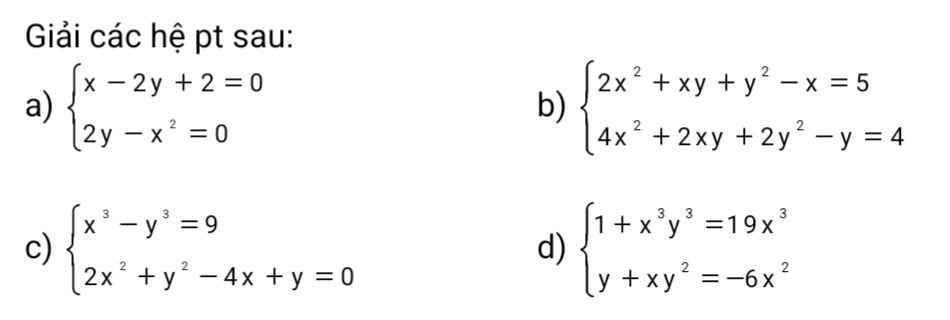b.
PT (1) $\Leftrightarrow (x+y)^2-2xy-3(x+y)=16(*)$
PT (2) $\Leftrightarrow xy=-7-(x+y)$. Thay vào $(*)$ thì:
$(x+y)^2-2[-7-(x+y)]-3(x+y)=16$
$\Leftrightarrow (x+y)^2+14-(x+y)=16$
$\Leftrightarrow (x+y)^2-(x+y)-2=0$
$\Leftrightarrow (x+y)^2+(x+y)-2(x+y)-2=0$
$\Leftrightarrow (x+y)(x+y+1)-2(x+y+1)=0$
$\Leftrightarrow (x+y+1)(x+y-2)=0$
$\Leftrightarrow x+y=-1$ hoặc $x+y=2$
Nếu $x+y=-1$ thì $xy=-7-(x+y)=-7-(-1)=-6$. Theo định lý Viet đảo thì $x,y$ là nghiệm của pt $X^2+X-6=0$
$\Rightarrow (x,y)=(2, -3), (-3,2)$
Nếu $x+y=2$ thì $xy=-7-(x+y)=-9$. Theo định lý Viet đảo thì $x,y$ là nghiệm của pt $X^2-2X-9=0$
$\Rightarrow (x,y)=(1+\sqrt{10}, 1-\sqrt{10}), (1-\sqrt{10}, 1+\sqrt{10})$
c.
Lấy PT(1) trừ PT(2):
$x^2-y^2-(3x-3y)=y^2-x^2$
$\Leftrightarrow 2(x^2-y^2)-(3x-3y)=0$
$\Leftrightarrow (x-y)(2x+2y-3)=0$
$\Leftrightarrow x-y=0$ hoặc $2x+2y-3=0$
Nếu $x-y=0\Rightarrow x=y$. Thay vào PT(1):
$x^2-3x=x^2+1\Leftrightarrow x=\frac{-1}{3}\Rightarrow y=\frac{-1}{3]$
Nếu $2x+2y-3=0\Leftrightarrow y=\frac{3-2x}{2}$. Thay vào PT(1):
$x^2-3x=(\frac{3-2x}{2})^2+1$
$\Leftrightarrow x^2-3x=(1,5-x)^2+1=3,25+x^2-3x$
$\Leftrightarrow 3,25=0$ (vô lý - loại)
a. Nếu $y=0$ thì $x=0$
Nếu $x=0$ thì $y=0$
Nếu $x,y\neq 0$:
$\frac{y-x}{4x+3y}=\frac{xy}{5xy}=\frac{1}{5}$
$\Rightarrow 5(y-x)=4x+3y$
$\Rightarrow 2y=9x\Rightarrow y=4,5x$. Thay vào PT(1):
$4,5x-x=x.4,5x$
$\Leftrightarrow 3,5x=4,5x^2$
$\Leftrightarrow x(3,5-4,5x)=0$
$\Leftrightarrow 3,5-4,5x=0$ (do $x\neq 0$)
$\Leftrightarrow x=\frac{7}{9}$
$y=4,5x=4,5.\frac{7}{9}=\frac{7}{2}$
d.
Lấy PT(1) trừ PT(2) theo vế:
2(x^2-y^2)=3(x-y)$
$\Leftrightarrow 2(x^2-y^2)-3(x-y)=0$
$\Leftrightarrow 2(x-y)(x+y)-3(x-y)=0$
$\Leftrightarrow (x-y)(2x+2y-3)=0$
$\Leftrightarrow x=y$ hoặc $2x+2y=3$
$\Leftrightarrow x=y$ hoặc $x=1,5-y$
Nếu $x=y$. Thay vào PT(1):
$2x^2+x^2=3x\Leftrightarrow 3x^2=3x\Leftrightarrow 3x(x-1)=0$
$\Leftrightarrow x=0$ hoặc $x=1$
$x=0$ thì $y=0$
$x=1$ thì $y=1$
Nếu $x=1,5-y$. Thay vào PT(1):
$2x^2+x(1,5-x)=3x$
$\Leftrightarrow x^2-1,5x=0\Leftrightarrow x(x-1,5)=0$
$\Rightarrow x=0$ hoặc $x=1,5$
$x=0\Rightarrow y=1,5-x=1,5$
$x=1,5\Rightarrow y=1,5-x=0$
e.
HPT \(\Leftrightarrow \left\{\begin{matrix} (x^2-x)+(y^2-2y)=19\\ x(x-1)y(y-2)=-20\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} (x^2-x)+(y^2-2y)=19\\ (x^2-x)(y^2-2y)=-20\end{matrix}\right.\)
Đặt $x^2-x=a; y^2-2y=b$ thì:
$a+b=19, ab=-20$
Khi đó theo định lý Viet đảo thì $a,b$ là nghiệm của PT:
$X^2-19X-20=0$
$\Leftrightarrow (X+1)(X-20)=0$
$\Rightarrow (a,b)=(-1,20), (20,-1)$
Nếu $a=-1, b=20$
$\Leftrightarrow x^2-x=-1; y^2-2y=20$
$x^2-x=-1\Leftrightarrow x^2-x+1=0$
$\Leftrightarrow (x-\frac{1}{2})^2=\frac{-3}{4}<0$ (vô lý - loại)
Nếu $a=20, b=-1$
$\Leftrightarrow x^2-x=20; y^2-2y=-1$
$\Leftrightarrow x^2-x-20=0; y^2-2y+1=0$
$\Leftrightarrow (x+4)(x-5)=0; (y-1)^2=0$
$\Rightarrow (x,y)=(-4,1), (5,1)$