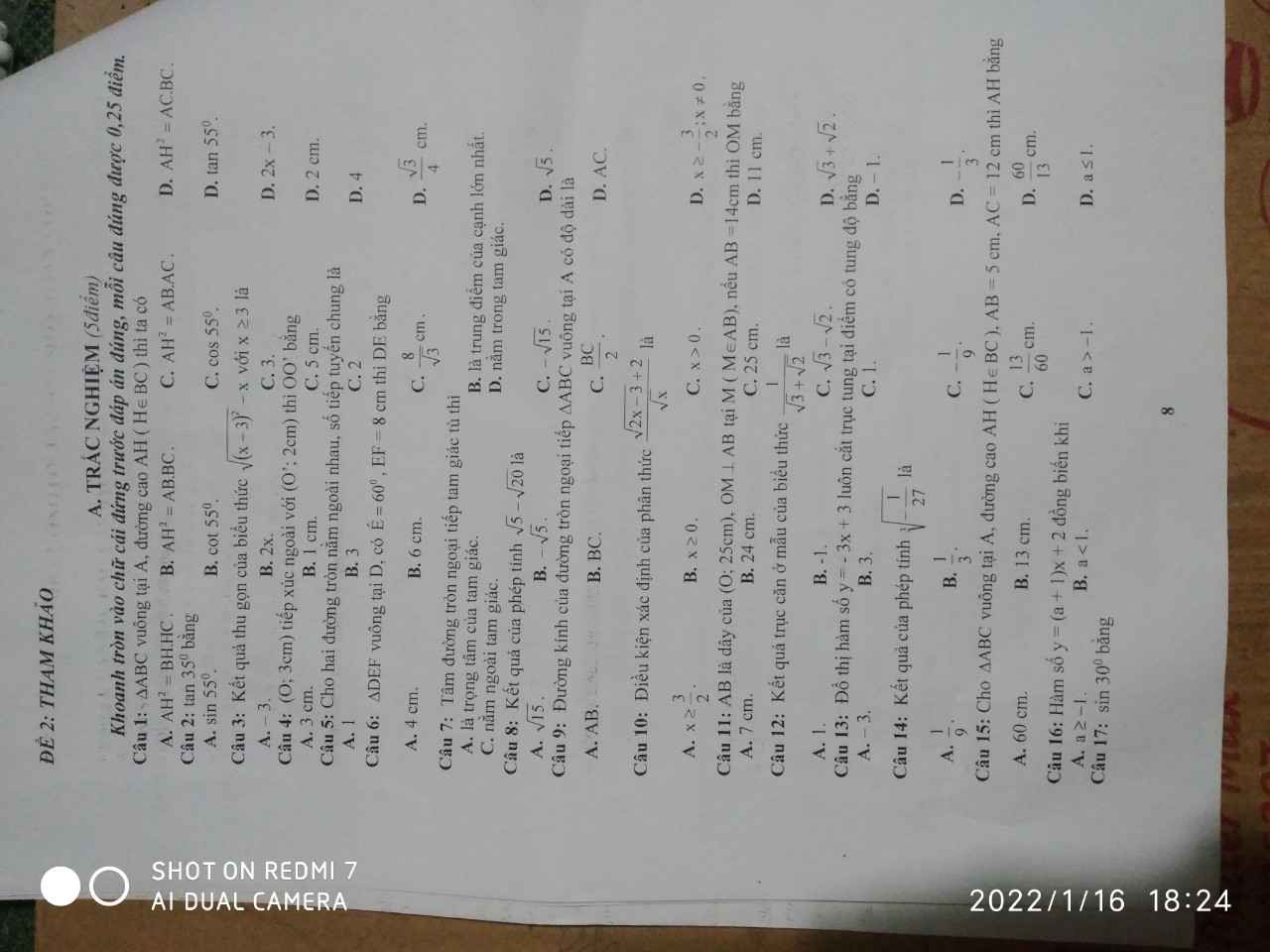
1: Thay x=4 vào A, ta được:
\(A=\dfrac{4-2}{2\cdot2+3}=\dfrac{2}{7}\)
2: \(B=\left(\dfrac{5\sqrt{x}}{x-4\sqrt{x}+3}+\dfrac{2}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}+2}{\sqrt{x}-3}\)
\(=\left(\dfrac{5\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-3\right)}-\dfrac{2}{\sqrt{x}-1}\right)\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}+2}\)
\(=\dfrac{5\sqrt{x}-2\sqrt{x}+6}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-3\right)}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}+2}\)
\(=\dfrac{3\sqrt{x}+6}{\sqrt{x}+2}\cdot\dfrac{1}{\sqrt{x}-1}=\dfrac{3}{\sqrt{x}-1}\)
3.
\(P=AB=\dfrac{x-\sqrt{x}}{2\sqrt{x}+3}.\dfrac{3}{\sqrt{x}-1}=\dfrac{3\sqrt{x}\left(\sqrt{x}-1\right)}{\left(2\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}=\dfrac{3\sqrt{x}}{2\sqrt{x}+3}\)
\(=\dfrac{6\sqrt{x}}{2\left(2\sqrt{x}+3\right)}=\dfrac{3\left(2\sqrt{x}+3\right)-9}{2\left(2\sqrt{x}+3\right)}=\dfrac{3}{2}-\dfrac{9}{2\left(2\sqrt{x}+3\right)}\)
P nhỏ nhất khi \(\dfrac{9}{2\left(2\sqrt{x}+3\right)}\) lớn nhất
\(\Rightarrow2\left(2\sqrt{x}+3\right)\) nhỏ nhất \(\Rightarrow x\) nhỏ nhất
Mà x là số nguyên dương và \(x\ne1\Rightarrow x=2\)
Khi đó: \(P_{min}=\dfrac{3\sqrt{2}}{2\sqrt{2}+3}\)
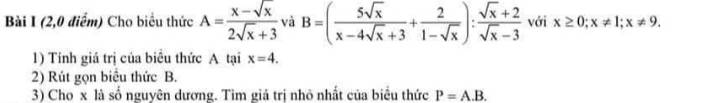
giúp tui bài 1 với :3
