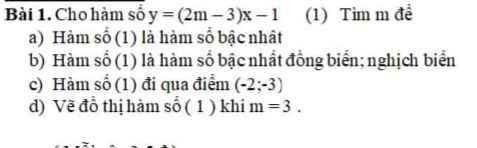`d)sqrt{7-2sqrt{10}}-sqrt{7+2sqrt{10}}`
`=sqrt{5-2sqrt{5}.sqrt2+2}-sqrt{5+2sqrt{5}.sqrt2+2}`
`=sqrt{(sqrt5-sqrt2)^2}-sqrt{(sqrt5+sqrt2)^2}`
`=sqrt5-sqrt2-sqrt5-sqrt2=-2sqrt2`
d, \(\sqrt{7-2\sqrt{10}}-\sqrt{7+2\sqrt{10}}=\sqrt{5-2.\sqrt{2}.\sqrt{5}+2}-\sqrt{5+2.\sqrt{2}.\sqrt{5}+2}\)
\(=\sqrt{\left(\sqrt{5}-\sqrt{2}\right)^2}-\sqrt{\left(\sqrt{5}+\sqrt{2}\right)^2}=\left|\sqrt{5}-\sqrt{2}\right|-\left|\sqrt{5}+\sqrt{2}\right|\)
\(=\sqrt{5}-\sqrt{2}-\sqrt{5}-\sqrt{2}=-2\sqrt{2}\)
d) Ta có: \(\sqrt{7-2\sqrt{10}}-\sqrt{7+2\sqrt{10}}\)
\(=\sqrt{5}-\sqrt{2}-\sqrt{5}-\sqrt{2}\)
\(=-2\sqrt{2}\)