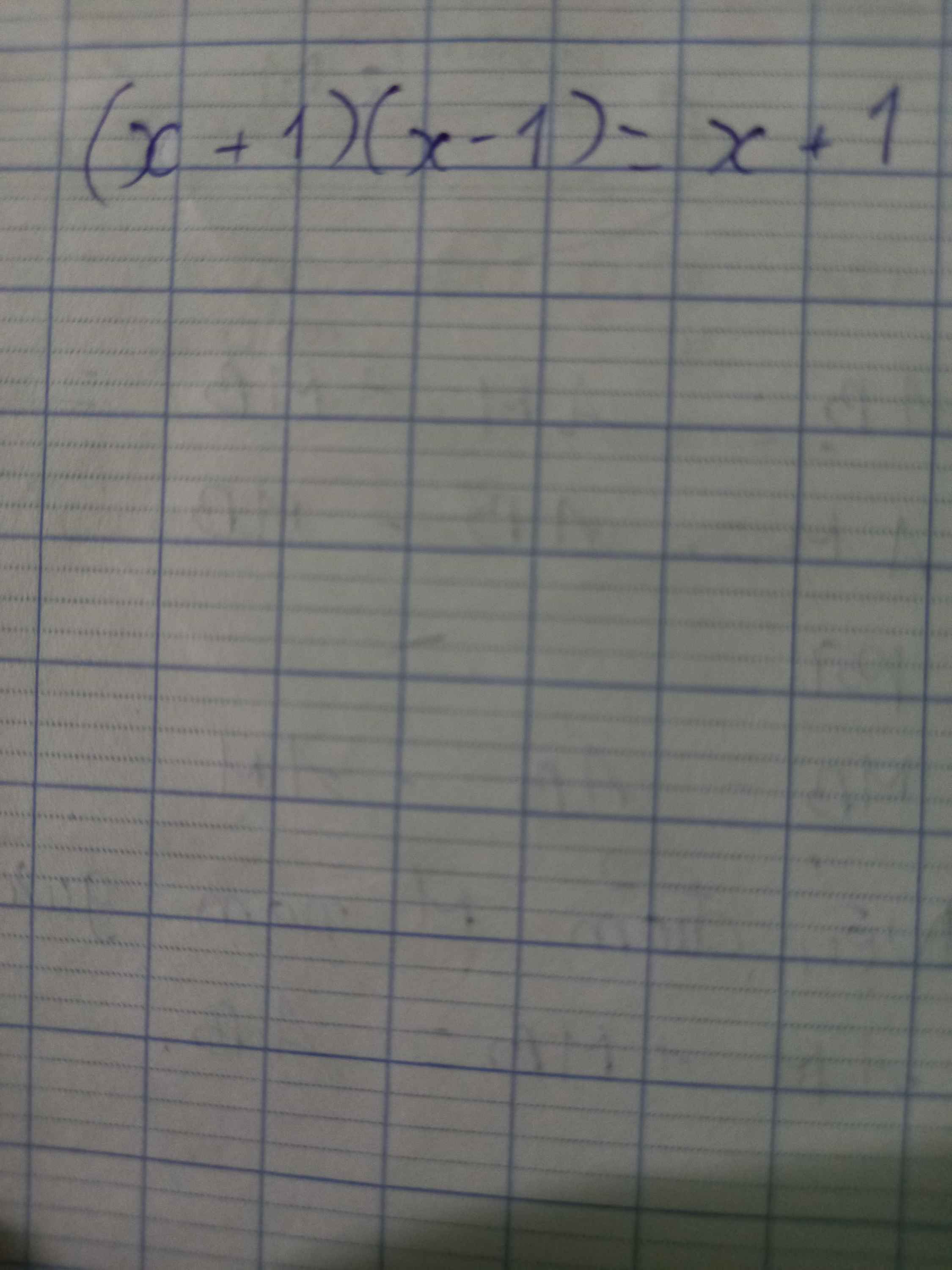a: \(A=\dfrac{4x^2-5x+1+4x^2+x+19-8x^2-8x-8}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{-12x+12}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{-12}{x^2+x+1}\)
b: Thay x=1/2 vào A, ta được:
\(A=\dfrac{-12}{\dfrac{1}{4}+\dfrac{1}{2}+1}=\dfrac{-12}{\dfrac{7}{4}}=-21\)
\(A=\dfrac{4x-1}{x^2+x+1}+\dfrac{4x^2+x+19}{x^2-1}+\dfrac{8}{1-x}\)
ĐKXĐ: x ≠ 1
\(A=\dfrac{\left(4x-1\right)\left(x-1\right)}{\left(x^2+x+x\right)\left(x-1\right)}+\dfrac{4x^2+x+19}{\left(x-1\right)\left(x^2+x+1\right)}-\dfrac{8\left(x^2+x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(A=\dfrac{4x^2-5x+1+4x^2+x+19-8x^2-8x-8}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(A=\dfrac{-12x+12}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(A=\dfrac{-12}{x^2+x+1}\)
\( \begin{array}{l} c) \ A=\frac{-12}{x^{2} +x+1}\\ Ta\ có:\ x^{2} +x+1=\left( x+\frac{1}{2}\right)^{2} +\frac{3}{4} \geqslant \frac{3}{4} \ \ \ \ \forall x\\ \Longrightarrow \ \frac{1}{x^{2} +x+1} \leqslant \frac{4}{3} \ \Longrightarrow \ \frac{-12}{x^{2} +x+1} \geqslant ( -12) .\frac{4}{3}\\ \Leftrightarrow \ A\geqslant -16\\ Vậy\ minA=-16\ đạt\ được\ \Leftrightarrow \ x=\frac{-1}{2} \ ( TM)\\ \end{array}\)
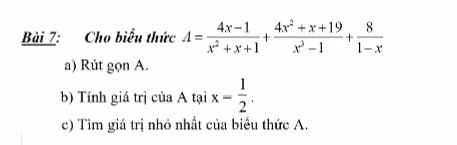
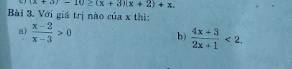
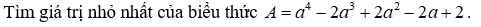
giúp mình với ạ mình cảm ơn
