\(A=\left(a^4-2a^3+a^2\right)+\left(a^2-2a+1\right)+1\)
\(A=\left(a^2-a\right)^2+\left(a-1\right)^2+1\ge1\)
\(A_{min}=1\) khi \(\left\{{}\begin{matrix}a^2-a=0\\a-1=0\end{matrix}\right.\) \(\Rightarrow a=1\)
Đúng 1
Bình luận (2)

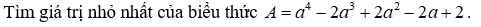











 giúp mình với ạ mình cảm ơn
giúp mình với ạ mình cảm ơn