a, đk : \(x\ne3\\ \)
\(\dfrac{x-2}{x-3}>0\\ \Leftrightarrow x-2>\\\Leftrightarrow x>2\)
Vậy \(x>2;x\ne3\)
b, đk : \(x\ne-\dfrac{1}{2}\)\
\(\dfrac{4x+3}{2x+1}< 2\\ \Leftrightarrow\dfrac{4x+3}{2x+1}-2< 0\\ \Leftrightarrow\dfrac{4x+3-2\left(2x+1\right)}{2x+1}< 0\\ \Leftrightarrow\dfrac{4x+3-4x-2}{2x+1}< 0\\ \Leftrightarrow\dfrac{1}{2x+1}< 0\)
vì \(1>0\)
\(\Rightarrow2x+1< 0\\ \Leftrightarrow x< -\dfrac{1}{2}\)
Vậy \(x< -\dfrac{1}{2}\)
Hquynh CTV: $\frac{x-2}{x-3}>0$ thì $x-2, x-3$ cùng dấu chứ không phải tương đương với $x-2>0$ bạn nhé.

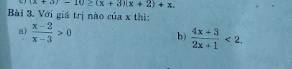





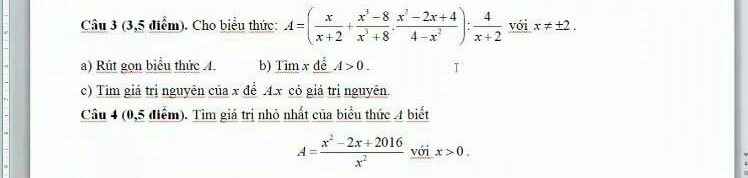

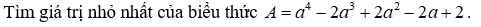




 giúp mình với ạ mình cảm ơn
giúp mình với ạ mình cảm ơn