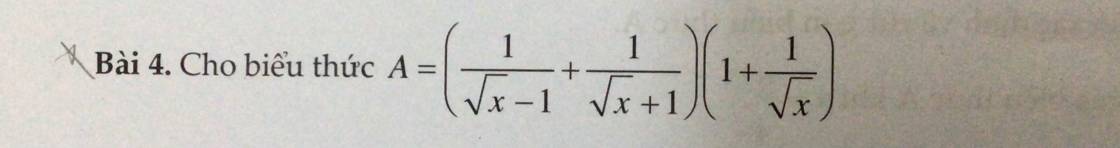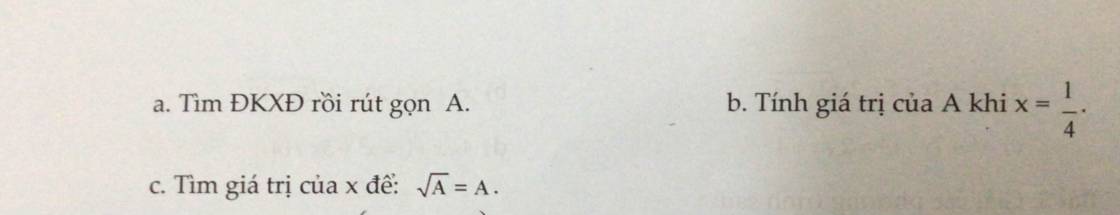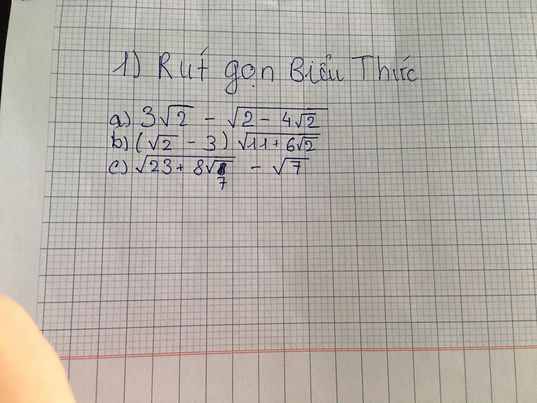ĐKXĐ: \(x\ge\frac12\)
\(\Leftrightarrow x^2-6x+2=4\sqrt{2x-1}-2x\sqrt{2x-1}\)
\(\Leftrightarrow x^2+2x\sqrt{2x-1}+2x-1=4\left(2x-1\right)+4\sqrt{2x-1}+1\)
\(\Leftrightarrow\left(x+\sqrt{2x-1}\right)^2=\left(2\sqrt{2x-1}+1\right)^2\)
\(\Rightarrow\left[\begin{array}{l}x+\sqrt{2x-1}=2\sqrt{2x-1}+1\\ x+\sqrt{2x-1}=-2\sqrt{2x-1}-1\end{array}\right.\)
\(\Rightarrow\left[\begin{array}{l}x-1=\sqrt{2x-1}\left(1\right)\\ x+1=-3\sqrt{2x-1}\left(2\right)\end{array}\right.\)
Pt (2) vô nghiệm do vế trái dương, vế phải âm khi \(x\ge\frac12\)
Xét pt (1), với \(x\le1\) pt vô nghiệm, với \(x>1\) bình phương 2 vế:
\(x^2-2x+1=2x-1\Rightarrow x^2-4x+2=0\Rightarrow x=2+\sqrt2\) (loại nghiệm ko thỏa đk)