b) \(\Delta=4\left(m+2\right)^2-4\left(m^2-4\right)=16m+32\)
Theo hệ thức Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=2m+4\left(2\right)\\x_1x_2=m^2-4\left(4\right)\end{matrix}\right.\)
Để pt (1) có hai nghiệm pb dương thì: \(\left\{{}\begin{matrix}\Delta >0\\x_1+x_2>0\\x_1x_2>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>-2\\\left[{}\begin{matrix}m< -2\\m>2\end{matrix}\right.\end{matrix}\right.\Leftrightarrow m>-2\)
Lại có: \(\dfrac{x_1}{x_2}-\dfrac{x_2}{x_1}=8\)
\(\Leftrightarrow\dfrac{x_1^2-x_2^2}{x_1x_2}=8\)
\(\Leftrightarrow\dfrac{\left(x_1-x_2\right)\left(x_1+x_2\right)}{x_1x_2}=8\)
\(\Leftrightarrow\dfrac{\left(x_1-x_2\right)\left(2m+4\right)}{m^2-4}=8\)
\(\Leftrightarrow\dfrac{2\left(x_1-x_2\right)\left(m+2\right)}{\left(m-2\right)\left(m+2\right)}=8\)
\(\Rightarrow2\left(x_1-x_2\right)=8\left(m-2\right)\)
\(\Leftrightarrow x_1-x_2=4m-8\) (3)
Kết hợp (2) và (3), ta có hệ: \(\left\{{}\begin{matrix}x_1+x_2=2m+4\\x_1-x_2=4m-8\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x_1=3m-2\\x_2=-m+6\end{matrix}\right.\)
Thay \(x_1=3m-2;x_2=-m+6\) vào (4), ta được:
\(\left(3m-2\right)\left(-m+6\right)=m^2-4\)
\(\Leftrightarrow-3m^2+20m-12-m^2+4=0\)
\(\Leftrightarrow-4m^2+20m-8=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{5+\sqrt{17}}{2}\left(tmdk\right)\\m=\dfrac{5-\sqrt{17}}{2}\left(tmdk\right)\end{matrix}\right.\)
$\text{#}Toru$


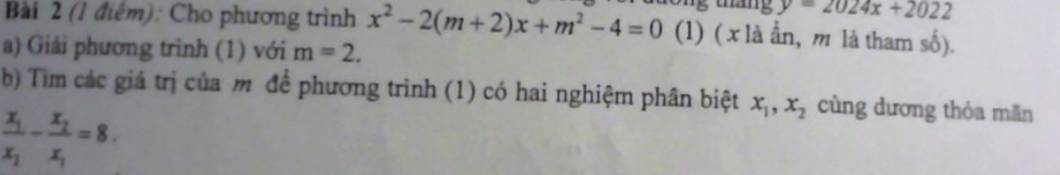
















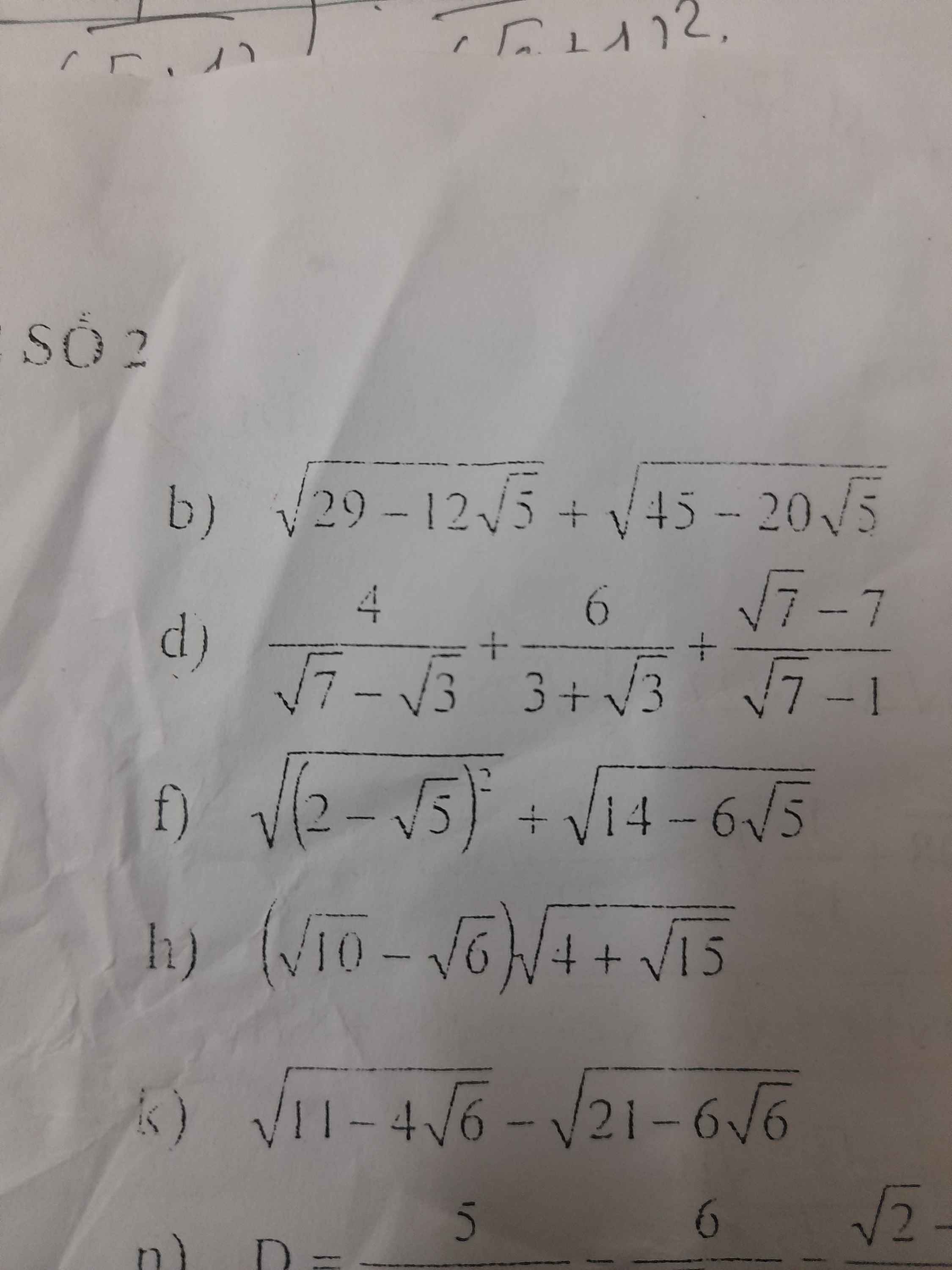

 giúp mình phần b với ạ
giúp mình phần b với ạ


