b) \(\sqrt{29-12\sqrt{5}}+\sqrt{45-20\sqrt{5}}=\sqrt{\left(2\sqrt{5}-3\right)^2}+\sqrt{\left(5-2\sqrt{5}\right)^2}=2\sqrt{5}-3+5-2\sqrt{5}=2\)
h) \(\left(\sqrt{10}-\sqrt{6}\right)\sqrt{4+\sqrt{15}}=\left(\sqrt{10}-\sqrt{6}\right)\sqrt{\left(\sqrt{\dfrac{5}{2}}+\sqrt{\dfrac{3}{2}}\right)^2}=\left(\sqrt{10}-\sqrt{6}\right)\left(\sqrt{\dfrac{5}{2}}+\sqrt{\dfrac{3}{2}}\right)=\sqrt{25}+\sqrt{15}-\sqrt{15}-\sqrt{9}=5-3=2\)
h: Ta có: \(\left(\sqrt{10}-\sqrt{6}\right)\cdot\sqrt{4+\sqrt{15}}\)
\(=\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+\sqrt{3}\right)\)
=5-3=2

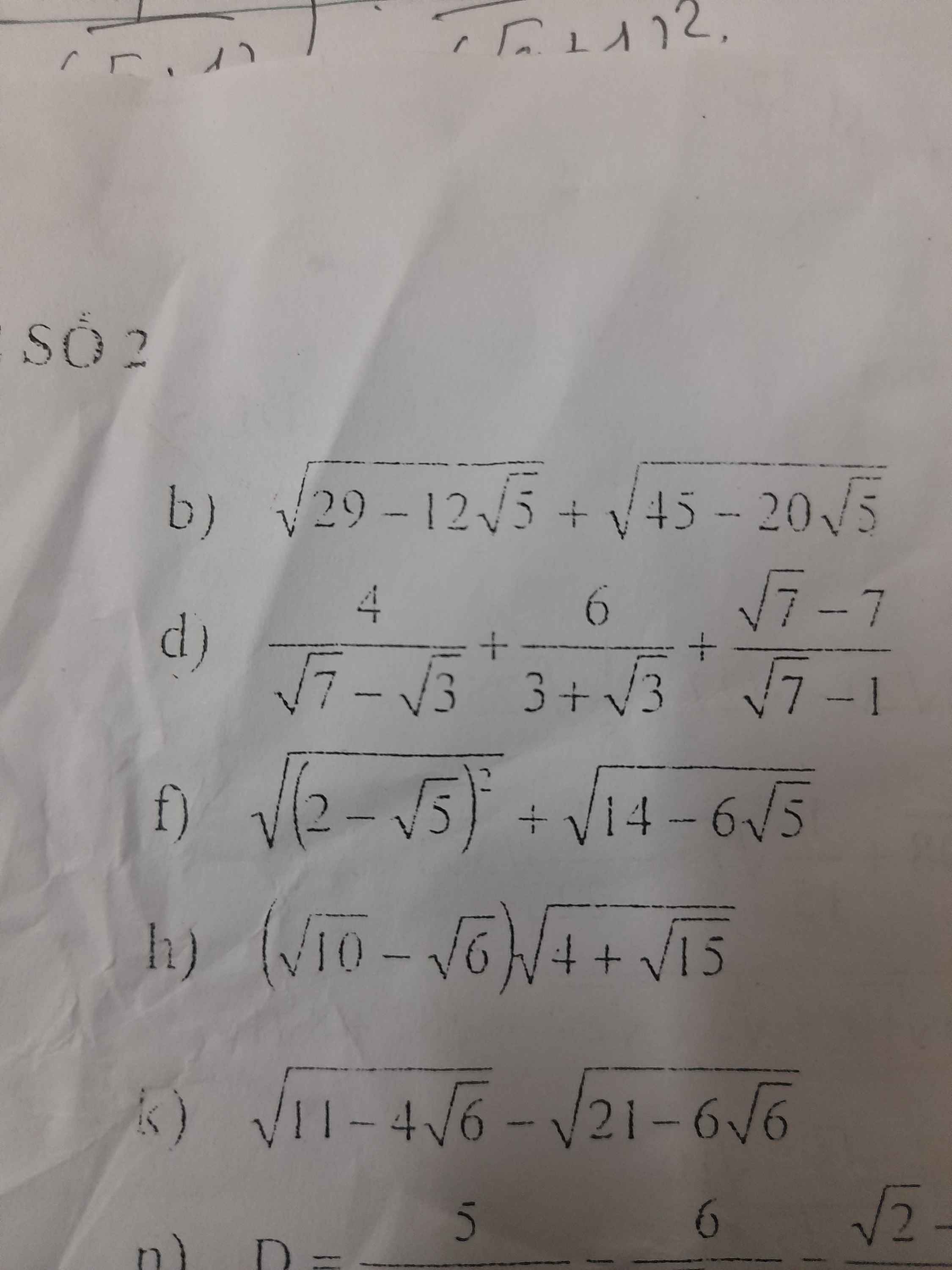

















 giúp em phần 7,8,9,12 bài 6 với ạ
giúp em phần 7,8,9,12 bài 6 với ạ



 giúp mình phần b với ạ
giúp mình phần b với ạ
