1: Xét tứ giác AMBO có
\(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)
nên AMBO là tứ giác nội tiếp
2: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1),(2) suy ra MO là đường trung trực của AB
=>MO\(\perp\)AB tại I
Xét (O) có
ΔAKC nội tiếp
AC là đường kính
Do đó: ΔAKC vuông tại K
=>AK\(\perp\)KC tại K
=>AK\(\perp\)MC tại K
Xét ΔMAC vuông tại A có AK là đường cao
nên \(MK\cdot MC=MA^2\left(3\right)\)
Xét ΔMAO vuông tại A có AI là đường cao
nên \(MI\cdot MO=MA^2\left(4\right)\)
Từ (3) và (4) suy ra \(MK\cdot MC=MI\cdot MO\)
=>\(\dfrac{MK}{MO}=\dfrac{MI}{MC}\)
Xét ΔMKI và ΔMOC có
\(\dfrac{MK}{MO}=\dfrac{MI}{MC}\)
góc KMI chung
Do đó: ΔMKI đồng dạng với ΔMOC
=>\(\widehat{MIK}=\widehat{MCO}=\widehat{ACM}\)






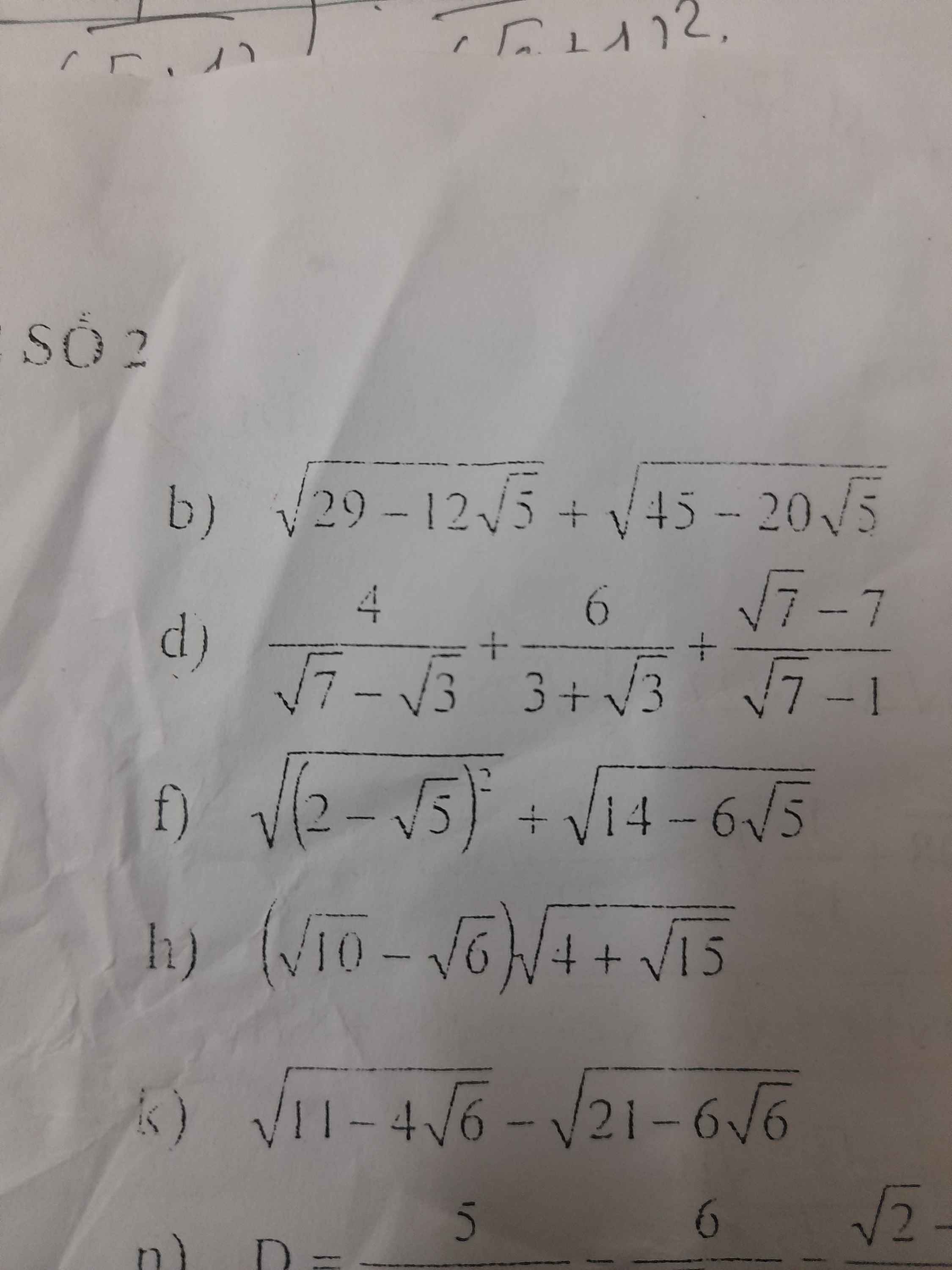









 Ai giúp em với ạ em cần rất gấp bài 4 thôi ạ
Ai giúp em với ạ em cần rất gấp bài 4 thôi ạ




