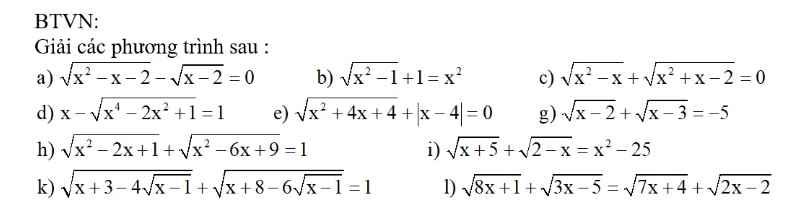1) Ta có: \(\sqrt{2x+5}=\sqrt{3-x}\)
\(\Leftrightarrow2x+5=3-x\)
\(\Leftrightarrow2x+x=3-5\)
\(\Leftrightarrow3x=-2\)
hay \(x=-\dfrac{2}{3}\)
2) Ta có: \(\sqrt{2x-5}=\sqrt{x-1}\)
\(\Leftrightarrow2x-5=x-1\)
\(\Leftrightarrow2x-x=-1+5\)
\(\Leftrightarrow x=4\)
3 , \(PT\left(đk:\frac{16}{3}\ge x\ge3\right)< =>x^2-3x=16-3x\)
\(< =>x^2-16=0< =>\left(x-4\right)\left(x+4\right)=0< =>\orbr{\begin{cases}x=4\left(tm\right)\\x=-4\left(ktm\right)\end{cases}}\)
4 , \(PT\left(đk:...\right)< =>2x^2-3=4x-3< =>2x^2-4x=0\)
\(< =>2x\left(x-2\right)=0< =>\orbr{\begin{cases}x=0\left(...\right)\\x=2\left(...\right)\end{cases}}\)
bạn tự tìm đk rồi đối chiếu nhé :P
5, \(PT\left(đk:...\right)< =>\left(2x-7\right)\left(x-2\right)=x-2\)
\(< =>\left(x-2\right)\left(2x-7-1\right)=0\)
\(< =>\orbr{\begin{cases}x=2\\2x-8=0\end{cases}< =>\orbr{\begin{cases}x=2\\x=4\end{cases}}}\)
6, \(PT\left(đk:...\right)< =>x^2-x-6=3x-1\)
\(< =>x^2-4x-5=0< =>\left(x-5\right)\left(x+1\right)=0\)
\(< =>\orbr{\begin{cases}x=5\\x=-1\end{cases}}\)
7 , \(PT\left(đk:...\right)< =>\sqrt{2x-3}.\sqrt{2x+3}=2\sqrt{2x+3}\)
\(< =>\sqrt{2x+3}.\left(\sqrt{2x-3}-2\right)=0\)
\(< =>\orbr{\begin{cases}x=-\frac{3}{2}\\2x-3=4\end{cases}}< =>\orbr{\begin{cases}x=-\frac{3}{2}\\x=\frac{7}{2}\end{cases}}\)
8, \(PT\left(đk:...\right)< =>\sqrt{2x-1}=\sqrt{x+2}.\sqrt{x-2}\)
\(< =>\sqrt{2x-1}=\sqrt{x^2-4}< =>x^2-2x-3=0\)
\(< =>\left(x+1\right)\left(x-3\right)=0< =>\orbr{\begin{cases}x=-1\\x=3\end{cases}}\)
9, \(PT\left(đk:...\right)< =>x-3=\sqrt{x-3}.\sqrt{x+1}\)
\(< =>\sqrt{x-3}\left(\sqrt{x-3}-\sqrt{x+1}\right)=0\)
\(< =>\orbr{\begin{cases}x=3\\x-3=x+1\end{cases}< =>\orbr{\begin{cases}x=3\\-4=0\left(vl\right)\end{cases}}}\)
\(\sqrt{9x^2-12x+4}=\sqrt{x^2}\left(đk:...\right)\)
\(< =>9x^2-12x+4=x^2< =>8x^2-12x+4=0\)
\(< =>2x^2-3x+1=0< =>2x^2-2x-\left(x-1\right)=0\)
\(< =>2x\left(x-1\right)-\left(x-1\right)=0< =>\left(2x-1\right)\left(x-1\right)=0\)
\(< =>\orbr{\begin{cases}2x-1=0\\x-1=0\end{cases}}< =>\orbr{\begin{cases}x=\frac{1}{2}\\x=1\end{cases}}\)
\(\sqrt{x^2-4x+4}=\sqrt{4x^2-12x+9}\left(đk:...\right)\)
\(< =>x^2-4x+4=4x^2-12x+9\)
\(< =>3x^2-8x+5=0< =>3x^2-3x-\left(5x-5\right)=0\)
\(< =>3x\left(x-1\right)-5\left(x-1\right)=0< =>\left(x-1\right)\left(3x-5\right)=0\)
\(< =>\orbr{\begin{cases}x-1=0\\3x-5=0\end{cases}< =>\orbr{\begin{cases}x=1\\3x=5\end{cases}< =>\orbr{\begin{cases}x=1\\x=\frac{5}{3}\end{cases}}}}\)