e: \(\Leftrightarrow\left\{{}\begin{matrix}10y=40\\4x+7y=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=4\\4x=-12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=4\\x=-3\end{matrix}\right.\)
\(d,\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2y+11}{3}\\\dfrac{4\left(2y+11\right)}{3}-5y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2y+11}{3}\\8y+44-15y=9\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2y+11}{3}\\-7y=-35\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{10+11}{3}=7\\y=5\end{matrix}\right.\)
\(e,\Leftrightarrow\left\{{}\begin{matrix}4x=16-7y\\16-7y-3y=-24\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x=16-7y\\10y=40\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}4x=16-7\cdot4=-12\\y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=4\end{matrix}\right.\)







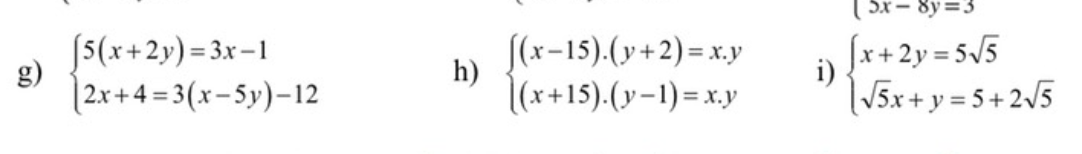



 Lập bảng và giải bằng hpt giúp e ạ
Lập bảng và giải bằng hpt giúp e ạ






