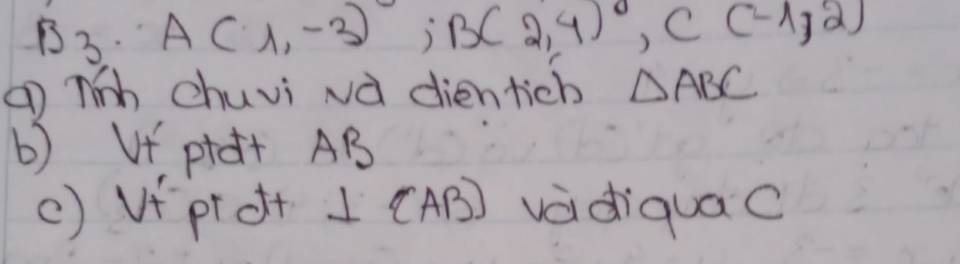f,Để \(\sqrt{4-x^2}\)có nghĩa
Thì\(4-x^2\ge0\)
\(\Leftrightarrow\left(2-x\right)\left(2+x\right)\ge0\)
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}2-x\ge0\\2+x\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}2-x\le0\\2+x\le0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\le2\\x\ge-2\end{matrix}\right.\\\left\{{}\begin{matrix}x\ge2\\x\le-2\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow-2\le x\le2\)
e, Để \(\sqrt{x^2+20}\) có nghĩa
thì\(x^2+20\ge0\)(luôn đúng với mọi x)
Vậy \(\sqrt{x^2+20}\)luôn có nghĩa
h,Để\(\sqrt{x^2+4x+4}\) có nghĩa
Thì \(x^2+4x+4\ge0\)
\(\Leftrightarrow\left(x+2\right)^2\ge0\)(với mọi x)
Vậy...
d) ĐKXĐ: x<-5
e) ĐKXĐ: \(x\in R\)
f) ĐKXĐ: \(-2\le x\le2\)
g) ĐKXĐ: x<0
h) ĐKXĐ: \(x\in R\)
i) ĐKXĐ: \(\left[{}\begin{matrix}x\ge2\\x< -1\end{matrix}\right.\)

 Giải giúp
Giải giúp





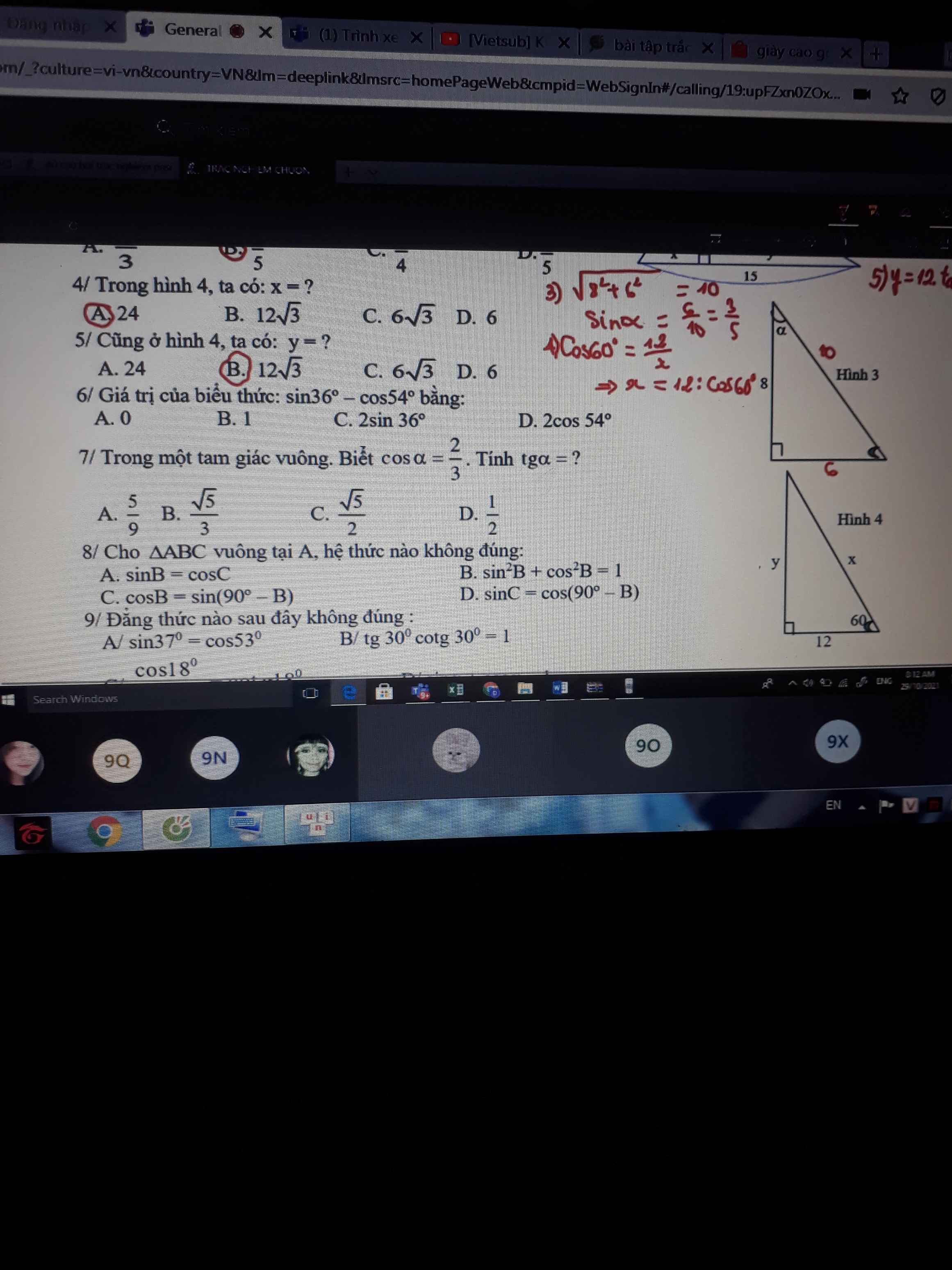






 Mọi người giúp mình với, giải chi tiết (+giải thích giúp mình nha), cảm ơn mọi người rất nhiều lun =)
Mọi người giúp mình với, giải chi tiết (+giải thích giúp mình nha), cảm ơn mọi người rất nhiều lun =)



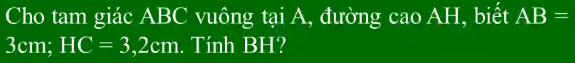



 giải giúp em ý nào cũng được ạ, giải chi tiết ạ
giải giúp em ý nào cũng được ạ, giải chi tiết ạ