Bài 4:\(x-y=2\Rightarrow\left(x-y\right)^2=4\Rightarrow x^2-2xy+y^2=4\Rightarrow x^2+y^2=4+2xy\)
\(A=2\left(x^3-y^3\right)-3\left(x+y\right)^2\)
\(A=2\left(x-y\right)\left(x^2+y^2+xy\right)-3\left(x^2+2xy+y^2\right)\)
\(A=2\left(x-y\right)\left(x^2+y^2+xy\right)-3\left(x^2-2xy+y^2+4xy\right)\)
\(A=2\left(x-y\right)\left(x^2+y^2+xy\right)-3\left[\left(x-y\right)^2+4xy\right]\)
\(A=2.2\left(4+2xy+xy\right)-3\left(2^2+4xy\right)\)
\(A=4\left(4+3xy\right)-3\left(4+4xy\right)\)
\(A=16+12xy-12-12xy=4\)
Vậy A=4
Bài 5:
a,\(\left(a+b\right)^2-\left(a-b\right)^2=a^2+2ab+b^2-\left(a^2-2ab+b^2\right)=a^2+2ab+b^2-a^2+2ab-b^2=4ab\)b,\(\left(a+b\right)^3-\left(a-b\right)^3-2b^3=\left(a^3+3a^2b+3ab^2+b^3\right)-\left(a^3-3a^2b+3ab^2-b^3\right)-2b^3=a^3+3a^2b+3ab^2+b^3-a^3+3a^2b-3ab^2+b^3-2b^3=6a^2b\)c,
\(\left(x+y+z\right)^2-2\left(x+y+z\right)\left(x+y\right)+\left(x^2+2xy+y^2\right)=x^2+y^2+z^2+2xy+2xz+2yz-\left(2x+2y+2z\right)\left(x+y\right)+x^2+2xy+y^2=2x^2+2y^2+z^2+4xy+2xz+2yz-2x^2-2xy-2xz-2xy-2y^2-2yz=\left(2x^2-2x^2\right)+\left(2y^2-2y^2\right)+z^2+\left(4xy-2xy-2xy\right)+\left(2xz-2xz\right)+\left(2yz-2yz\right)=z^2\)
Bài 2:
b: \(\left(5-3x\right)^2=5^2-2\cdot5\cdot3x+\left(3x\right)^2\)
\(=25-30x+9x^2\)
a: \(\left(2+xy\right)^2=\left(xy\right)^2+2\cdot xy\cdot2+2^2\)
\(=x^2y^2+4xy+4\)
d: \(\left(x+3\right)\left(x^2-3x+9\right)=x^3+3^3=x^3+27\)
c: \(\left(5x-1\right)^3=\left(5x\right)^3-3\cdot\left(5x\right)^2\cdot1+3\cdot5x\cdot1^2-1^3\)
\(=125x^3-75x^2+15x-1\)
d: \(\left(2x-y\right)\left(4x^2+2xy+y^2\right)\)
\(=\left(2x\right)^3-y^3=8x^3-y^3\)
e: \(\left(5-x^2\right)\left(5+x^2\right)=5^2-\left(x^2\right)^2=25-x^4\)
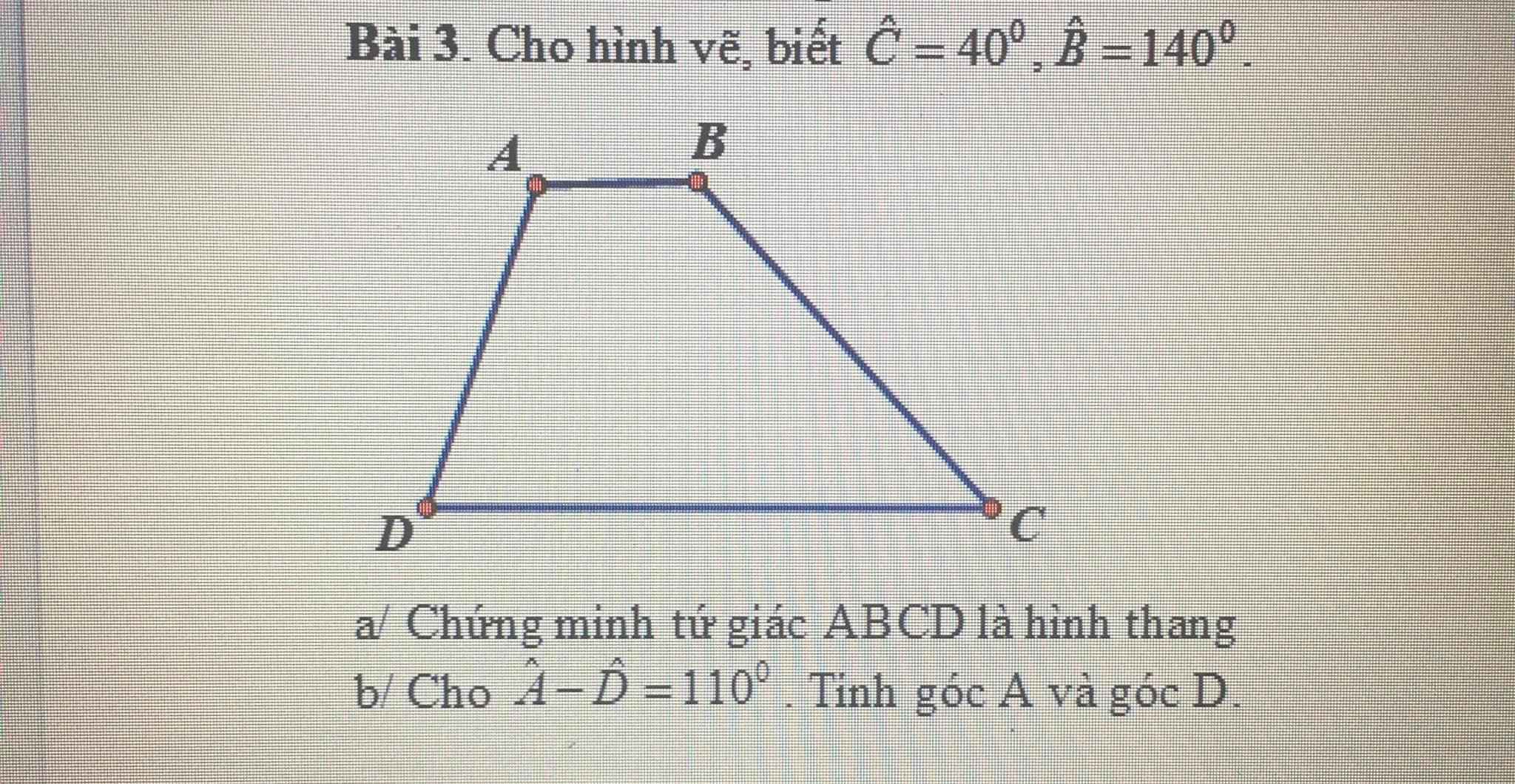
Bài 3:
a: \(34^2+66^2+68\cdot66\)
\(=34^2+2\cdot34\cdot66+66^2\)
\(=\left(34+66\right)^2=100^2=10000\)
b: \(74^2+24^2-48\cdot74\)
\(=74^2-2\cdot74\cdot24+24^2\)
\(=\left(74-24\right)^2=50^2=2500\)
c: \(136^2-92\cdot136+46^2\)
\(=136^2-2\cdot136\cdot46+46^2\)
\(=\left(136-46\right)^2=90^2=8100\)
d: \(263^2+74\cdot263+37^2\)
\(=263^2+2\cdot263\cdot37+37^2\)
\(=\left(263+37\right)^2=300^2=90000\)
e: \(\left(50^2+48^2+...+2^2\right)-\left(49^2+47^2+...+1^2\right)\)
\(=\left(50^2-49^2\right)+\left(48^2-47^2\right)+...+\left(2^2-1^2\right)\)
\(=\left(50-49\right)\left(50+49\right)+\left(48-47\right)\left(48+47\right)+...+\left(2-1\right)\left(2+1\right)\)
=50+49+...+2+1
\(=50\cdot\dfrac{51}{2}=25\cdot51=1225\)

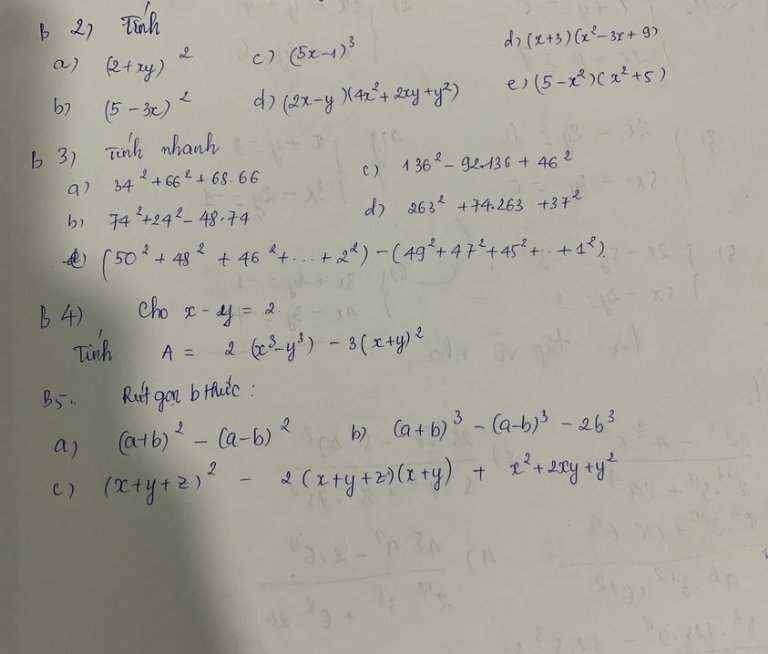 giải giúp mình ,mình cần gấp ạ!!!
giải giúp mình ,mình cần gấp ạ!!!