`a) 4^(x-2) + 4^(x+1) = 1040`
`=> 4^(x-2) + 4^(x-2) . 4^2 = 1040`
`=> 4^(x-2) . (1 + 64) = 1040`
`=> 4^(x-2) . 65 = 1040`
`=> 4^(x-2) = 16`
`=> 4^(x-2) = 4^2`
`=> x - 2 = 2`
`=> x = 4`
Vậy `x = 4`
\(a,4^{x-2}+4^{x+1}=1040\\ =>4^{x-2}\cdot\left(1+4^3\right)=1040\\ =>4^{x-2}\cdot65=1040\\ =>4^{x-2}=\dfrac{1040}{65}\\ =>4^{x-2}=16\\ =>4^{x-2}=4^2\\ =>x-2=2\\ =>x=2+2=4\\ d,2^{x+1}\cdot3^y=12^x\\ =>2^{x+1}\cdot3^y=\left(2^2\right)^x\cdot3^x\\ =>2^{x+1}\cdot3^y=2^{2x}\cdot3^x\\ =>\left\{{}\begin{matrix}x+1=2x\\y=x\end{matrix}\right.\\ =>x=y=1\\ d,\left(x-5\right)^2=\left(1-3x\right)^2\\ TH1:x-5=1-3x\\ =>x+3x=5+1\\ =>4x=6\\ =>x=\dfrac{3}{2}\\ TH2:x-5=3x-1\\ =>3x-x=-5+1\\ =>2x=-4\\ =>x=\dfrac{-4}{2}=-2\)
\(a.4^{x-2}+4^{x+1}=1040\)
\(4^x:4^2+4^x.4=1040\)
\(4^x:16+4^x.4=1040\)
\(4^x.\dfrac{1}{16}+4^x.4=1040\)
\(4^x\left(\dfrac{1}{16}+4\right)=1040\)
\(4^x.\dfrac{65}{16}=1040\)
\(4^x=1040:\dfrac{65}{16}\)
\(4^x=1040.\dfrac{16}{65}\)
\(4^x=256\)
\(4^x=4^4\)
\(x=4\)
Vậy \(x=4\)
`(x-5)^2 = (1-3x)^2`
`=> x - 5 = 1 - 3x hoặc `x - 5 = 3x - 1`
`=> 4x = 6` hoặc `2x = -4`
`=> x = 3/2` hoặc `x = -2`
Vậy ...
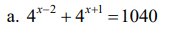
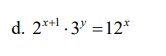
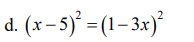
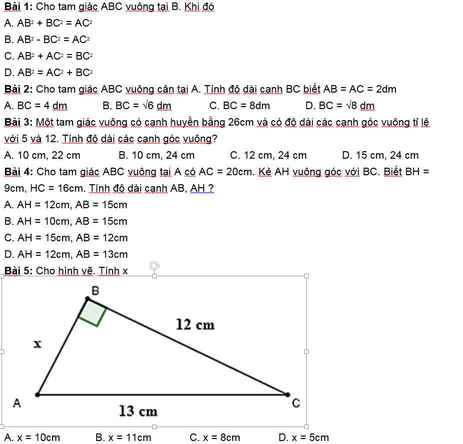
Giải chi tiết hộ mình nha!!!
