\(2x-3\sqrt{2x-1}=5\)
\(ĐK:x\ge\dfrac{1}{2}\)
\(\Leftrightarrow2x-1-3\sqrt{2x-1}=4\)
Đặt \(\sqrt{2x-1}=a;a\ge0\)
ptr trở thành:
\(\Leftrightarrow a^2-3a-4=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=1\left(ktm\right)\\a=4\left(tm\right)\end{matrix}\right.\)
`a=4`\(\Rightarrow\sqrt{2x-1}=4\)
\(\Leftrightarrow2x-1=16\)
\(\Leftrightarrow x=\dfrac{17}{2}\left(tm\right)\)
Vậy \(S=\left\{\dfrac{17}{2}\right\}\)

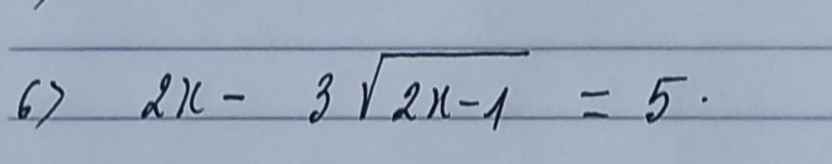








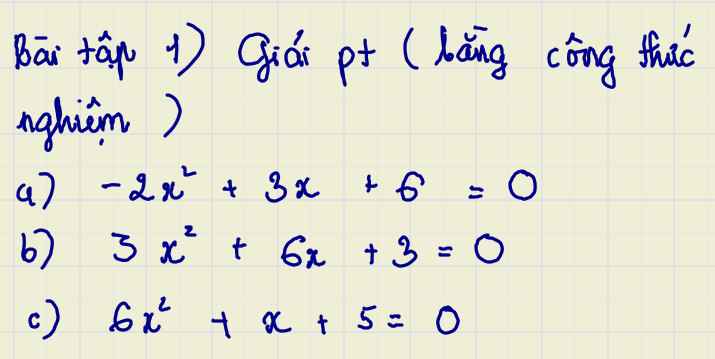

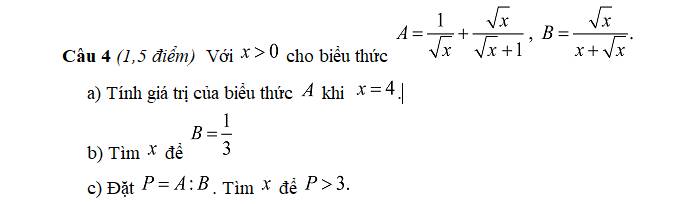

 Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn
Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn

