d) \(\dfrac{x-5}{3}< \dfrac{x-8}{4}\Rightarrow\dfrac{4\left(x-5\right)}{12}< \dfrac{3\left(x-8\right)}{12}\Rightarrow4x-20< 3x-24\Rightarrow x< -4\)
e) \(\dfrac{x+3}{4}+1< x+\dfrac{x+2}{3}\Rightarrow\dfrac{x+3+4}{4}< \dfrac{3x+x+2}{3}\Rightarrow\dfrac{x+7}{4}< \dfrac{4x+2}{3}\Rightarrow\dfrac{3\left(x+7\right)}{12}< \dfrac{4\left(4x+2\right)}{12}\Rightarrow3x+21< 16x+8\Rightarrow-13x< -13\Rightarrow x>1\)
d. \(\dfrac{x-5}{3}< \dfrac{x-8}{4}\)
\(\Leftrightarrow4\left(x-5\right)< 3\left(x-8\right)\)
\(\Leftrightarrow4x-20< 3x-24\)
\(\Leftrightarrow4x-3x< -24+20\)
\(\Leftrightarrow x< -4\)
e. \(\dfrac{x+3}{4}+1< x+\dfrac{x+2}{3}\)
\(\Leftrightarrow\dfrac{x+3+4}{4}< \dfrac{3x+x+2}{3}\)
\(\Leftrightarrow3\left(x+7\right)< 4\left(4x+2\right)\)
\(\Leftrightarrow3x+21< 16x+8\)
\(\Leftrightarrow3x-16x< 8-21\)
\(\Leftrightarrow-13x< -13\)
\(\Leftrightarrow x>1\)
#$\mathtt{Toru}$

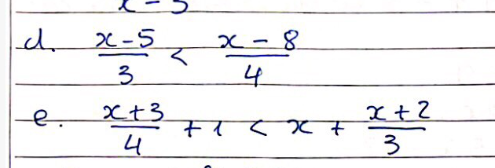 giải BPT sau
giải BPT sau