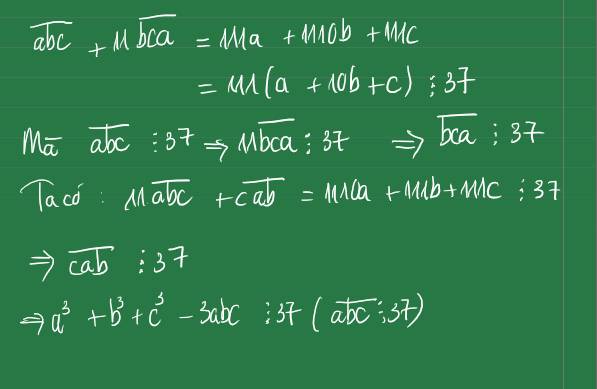Các câu hỏi tương tự
CMR nếu số tự nhiên abc chia hết cho 37 thì bca và cab cũng chia hết cho 37
Cho S= abc+bca+cab ( các số này là các số có 3 chữ số)
Chứng tỏ S chia hết cho 37.
Tìm số tự nhiên \(\overline{abc}\) sao cho khi lấy \(\overline{abc}:11\) được thương là tổng của \(a+b+c\)
1.Chứng minh rằng: left(x^m+x^n+1right)chia hết cho x^2+x+12.Tìm một số có 8 chữ số: overline{a_1a_2....a_8}thỏa mãn 2 điều kiện a và b sau:a) overline{a_1a_2a_3}left(overline{a_7a_8}right)^2 b) overline{a_4a_5a_6a_7a_8}left(overline{a_7a_8}right)^3Các thánh giải bài này giúp mik nha!
Đọc tiếp
1.Chứng minh rằng: \(\left(x^m+x^n+1\right)\)chia hết cho \(x^2+x+1\)
2.Tìm một số có 8 chữ số: \(\overline{a_1a_2....a_8}\)thỏa mãn 2 điều kiện a và b sau:
a) \(\overline{a_1a_2a_3}=\left(\overline{a_7a_8}\right)^2\) b) \(\overline{a_4a_5a_6a_7a_8}=\left(\overline{a_7a_8}\right)^3\)
Các thánh giải bài này giúp mik nha!
Khi tham gia sinh hoạt CLB Toán bạn Việt nhận đc thông báo sau:tài khoàn wifi của CLB có mật khẩu là:math1xyz ,trong đó số tự nhiên xyz là kết quả bài toán sau:Khi chia số tự nhiên m cho 5 đc số dư là a , m chia chia hết cho 6 đc thương là b.Biết tổng của a và b là 11 và xyz là tổng tất cả các số tự nhiên m thỏa các điều kiện trên.a)Viết tập hợp A các số tự nhiên a thỏa yêu cầu trên.b)Mật khẩu đầy đủ của tài khoản CLB Toán là gì?Giải thích.
Đọc tiếp
Khi tham gia sinh hoạt CLB Toán bạn Việt nhận đc thông báo sau:tài khoàn wifi của CLB có mật khẩu là:math1xyz ,trong đó số tự nhiên xyz là kết quả bài toán sau:
Khi chia số tự nhiên m cho 5 đc số dư là a , m chia chia hết cho 6 đc thương là b.Biết tổng của a và b là 11 và xyz là tổng tất cả các số tự nhiên m thỏa các điều kiện trên.
a)Viết tập hợp A các số tự nhiên a thỏa yêu cầu trên.
b)Mật khẩu đầy đủ của tài khoản CLB Toán là gì?Giải thích.
Tìm các chữ số a, b, c đôi một khác nhau thỏa mãn
\(\overline{acb}+\overline{cab}=2\overline{abc}\) và b>c
Hãy tính số bị chia, số chia và thương trong phép chia sau đây:
\(\overline{abcd}:\overline{dcba}=q\)Biết cả 3 số đều là bình phương của những số nguyên và a;b;c;d khác nhau đôi một
Chứng minh có vô số các số tự nhiên n sao cho \(\overline{2016n}\) là số chính phương
câu 1 :chứng minh : nn-n^2+n-1 chia hết cho (n-1)^2 với n là số nguyên lớn hơn 1
câu 2 : chứng minh với n lẻ n thuộc N* thì 1^n+2^n+3^n+...+n^n chia hết cho 1+2+3+...+n
câu3: có tồn tại số tự nhiên n để n^2+3n+39 và n^2+n+37 đồng thời chia hết cho 49 không?