Các câu hỏi tương tự
cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Gọi E, F lần lượt là trung điểm SA, SD
a) đường thẳng BD và (ABCD)
b) đường thẳng BD và (SCD)
c) đường thẳng EF và (ABCD)
d) đường thẳng EF và (SAB)
e) đường thẳng EF và (SAD)
Cho hình chóp S.ABCD, có đáy ABCD là hình thang có đáy lớn AD . Gọi E, F lần lượt là trung điểm của SA, SD.a) Tìm giao tuyến của các cặp mặt phẳng: (SAC) và (SBD), (SAD) và (SBC).b) Chứng minh EF// (ABCD) và EF// (SBC) c) Gọi K là giao điểm của AB và CD. Tìm M, N lần lượt là giao điểm của SB và (CDE); SC và (EFM). Từ đó, tìm thiết diện của hình chóp cắt bởi mặt phẳng (KEF)d) Cho AD2BC. Tính tỉ số diện tích của tam giác KMN và tam giác KEF .giúp mình giải câu d với ạ
Đọc tiếp
Cho hình chóp S.ABCD, có đáy ABCD là hình thang có đáy lớn AD . Gọi E, F lần lượt là trung điểm của SA, SD.
a) Tìm giao tuyến của các cặp mặt phẳng: (SAC) và (SBD), (SAD) và (SBC).
b) Chứng minh EF// (ABCD) và EF// (SBC)
c) Gọi K là giao điểm của AB và CD. Tìm M, N lần lượt là giao điểm của SB và (CDE); SC và (EFM). Từ đó, tìm thiết diện của hình chóp cắt bởi mặt phẳng (KEF)
d) Cho AD=2BC. Tính tỉ số diện tích của tam giác KMN và tam giác KEF .
giúp mình giải câu d với ạ
Cho chóp SABC có đáy là tam giác ABC vuông tại B có sa vuông (ABC) (.) Tam giác sab và sac kẻ dường cao AH vuông AB và AK vuông SC C/m AH vuông ( SBC), AHK vuông SAC, EA vuông AC
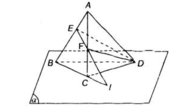
Cho điểm A không nằm trên mặt phẳng (α) chứa tam giác BCD. Lấy E và F là các điểm lần lượt nằm trên các cạnh AB , AC.a) Chứng minh đường thẳng EF nằm trong mặt phẳng (ABC).b) Giả sử EF và BC cắt nhau tại I, chứng minh I là điểm chung của hai mặt phẳng (BCD) và (DEF).
Đọc tiếp
Cho điểm A không nằm trên mặt phẳng (α) chứa tam giác BCD. Lấy E và F là các điểm lần lượt nằm trên các cạnh AB , AC.
a) Chứng minh đường thẳng EF nằm trong mặt phẳng (ABC).
b) Giả sử EF và BC cắt nhau tại I, chứng minh I là điểm chung của hai mặt phẳng (BCD) và (DEF).
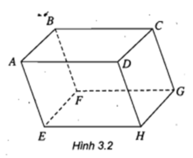
Cho hình hộp ABCD.EFGH. Hãy thực hiện các phép toán sau đây (h.3.2):a)
A
B
→
+
C
D
→
+
E
F
→
+
G
H
→
b)
B...
Đọc tiếp
Cho hình hộp ABCD.EFGH. Hãy thực hiện các phép toán sau đây (h.3.2):
a) A B → + C D → + E F → + G H →
b) B E → - C H →
Thị xã Từ Sơn xây dựng một ngọn tháp đèn lộng lẫy hình chóp tứ giác đều S.ABCD có cạnh bên SA 12m và
A
S
B
^
30
0
. Người ta cần mặc một đường dây điện từ điểm A đến trung điểm K của SA gồm 4 đoạn thẳng AE, EF, FH, HK như hình vẽ. Để tiết kiệm chi phí ngừơi ta cần thiết kế được chiều dài con đường từ A đến K là ngắn nhất. Tính tỉ số K ...
Đọc tiếp
Thị xã Từ Sơn xây dựng một ngọn tháp đèn lộng lẫy hình chóp tứ giác đều S.ABCD có cạnh bên SA = 12m và A S B ^ = 30 0 . Người ta cần mặc một đường dây điện từ điểm A đến trung điểm K của SA gồm 4 đoạn thẳng AE, EF, FH, HK như hình vẽ. Để tiết kiệm chi phí ngừơi ta cần thiết kế được chiều dài con đường từ A đến K là ngắn nhất. Tính tỉ số K = H F + H K E A + E F
A . k = 3 4
B . k = 1 2
C . k = 1 3
D . k = 2 3
Cho hình lăng trụ tứ giác ABCD.A'B'C'D' có E, F, M và N lần lượt là trung điểm của AC, BD, AC' và BD'. Chứng minh MN = EF.
Cho hình chóp S.ABCD có đáy là hình thang ABCD (đáy lớn AB). Gọi E, F lần lượt là trung điểm của SA và SB. Chứng minh EF // CD
Cho hình chóp S.ABCD có đáy là hình thang ABCD với đáy là AD và BC. Biết AD a, BC b. Gọi I và J lần lượt là trọng tâm của các tam giác SAD và SBC. Mặt phẳng (ADJ) cắt SB, SC lần lượt tại M, N. Mặt phẳng (BCI) cắt SA, SD lần lượt tại P, Q.a) Chứng minh MN song song với PQ.b) Giả sử AM cắt BP tại E; CQ cắt DN tại F. Chứng minh rằng EF song song với MN và PQ. Tính EF theo a và b.
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang ABCD với đáy là AD và BC. Biết AD = a, BC = b. Gọi I và J lần lượt là trọng tâm của các tam giác SAD và SBC. Mặt phẳng (ADJ) cắt SB, SC lần lượt tại M, N. Mặt phẳng (BCI) cắt SA, SD lần lượt tại P, Q.
a) Chứng minh MN song song với PQ.
b) Giả sử AM cắt BP tại E; CQ cắt DN tại F. Chứng minh rằng EF song song với MN và PQ. Tính EF theo a và b.






