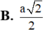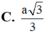a: \(D\in BD;D\in\left(ABCD\right)\)
Do đó: \(D\in BD\cap\left(ABCD\right)\)
\(B\in BD;B\in\left(ABCD\right)\)
=>\(B\in BD\cap\left(ABCD\right)\)
Do đó: \(BD\cap\left(ABCD\right)=DB\)
b: \(D\in BD;D\in\left(SCD\right)\)
=>\(D=BD\cap\left(SCD\right)\)
c: Xét ΔSAD có \(\dfrac{SE}{SA}=\dfrac{SF}{SD}\)
nên EF//AD
=>EF//(ABCD)
e: EF//AD
\(AD\subset\left(SAD\right)\)
Do đó: EF//(SAD)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và AB =2a, BC =a. Các cạnh bên của hình chóp bằng nhau và bằng a 2 . Gọi E và F lần lượt là trung điểm của AB và CD; K là điểm bất kỳ trên BC. Khoảng cách giữa hai đường thẳng EF và SK là:
A. a 3 3
B. a 6 3
C. a 15 5
D. a 21 7
cho hình chóp S.ABCD, đáy ABCD là hình thang, có đáy lớn AB. Gọi M,N lần lượt là trung điểm SA,SC; E = AC giao BD. Xác định vị trí tương đối của các cặp đường thẳng và mặt phẳng sau
a) MN và (ABCD)
b) AN và (ABD)
c) SE và (SAC)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật biết AB=a; AD= 2a; SA vuông góc với đáy, SA=a√2. Xác định và tính góc giữa. a) Các đường thẳng SB, SC, SD với mp đáy. b) SC với các mp (SAD) và ( SAB). c) SA với mp (SCD). d) SB và (SAC).
Cho hình chóp S.ABCD có SA ⊥ (ABCD) đáy ABCD là hình thang vuông có chiều cao AB=a Gọi I và J lần lượt là trung điểm AB,CD . Tính khoảng cách giữa đường thẳng IJ và (SAD).
Cho hình chóp S.ABCD, có đáy ABCD là hình thang có đáy lớn AD . Gọi E, F lần lượt là trung điểm của SA, SD.
a) Tìm giao tuyến của các cặp mặt phẳng: (SAC) và (SBD), (SAD) và (SBC).
b) Chứng minh EF// (ABCD) và EF// (SBC)
c) Gọi K là giao điểm của AB và CD. Tìm M, N lần lượt là giao điểm của SB và (CDE); SC và (EFM). Từ đó, tìm thiết diện của hình chóp cắt bởi mặt phẳng (KEF)
d) Cho AD=2BC. Tính tỉ số diện tích của tam giác KMN và tam giác KEF .
giúp mình giải câu d với ạ
cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O. Gọi M. N, E lần lượt là trung điểm CD, AB, SA
a) đường thẳng MN song song với (SAD)
b) đường thẳng BC song song với (EMN)
c) đường thẳng AD song song với (EMN)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J, E, F lần lượt là trung điểm SA, SB, SC, SD. Trong các đường thẳng sau, đường thẳng nào không song song với IJ?
A. EF
B. CD
C. AD
D. AB
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh SA ⊥ (ABCD) và SA = 3a.
a) Chứng minh AD ⊥ (SAB) và AB ⊥ (SAD)
b) Kẻ đường cao AM trong tam giác SAB. Chứng minh rằng AM ⊥ SC
c) Tính góc giữa đường thẳng SB và (SAC)
cho hình chóp s.abcd có đáy abcd là hình bình hành. gọi i,j,k theo thứ tự là trung điểm của các cạnh ab, cd và sa. a) tìm giao tuyến của hai mp (SAB)và(SCD) b) CM: IJ // (SCD) c) tìm giao điểm của đường thẳng SD với mp(IJK)
