Đáp án D
![]()
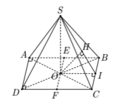
I là trung điểm cạnh đáy BC. Do SA = SB = SC = SD nên SO ⊥ (ABCD)
Từ đó ta chứng minh được
![]()
![]()
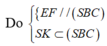
![]()
Tính được
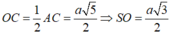
Suy ra
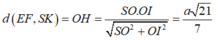
Đáp án D

![]()
I là trung điểm cạnh đáy BC. Do SA = SB = SC = SD nên SO ⊥ (ABCD)
Từ đó ta chứng minh được
![]()
![]()
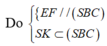
![]()
Tính được
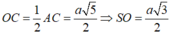
Suy ra
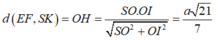
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=2a, BC=a. Các cạnh bên của hình chóp bằng nhau và bằng a 2 . Gọi M, N lần lượt là trung điểm của các cạnh AB, CD. K là điểm trên cạnh AD sao cho KD=2KA. Tính khoảng cách giữa hai đường thẳng MN và SK.
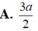
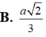
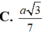
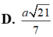
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB=2a, BC=a. Các cạnh bên của hình chóp cùng bằng a 2 . Tính góc giữa hai đường thẳng AB và SC.
A. 45 °
B. 30 °
C. 60 °
D. arctan 2
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 2a, BC =a. Hình chiếu vuông góc H của đỉnh S trên mặt phẳng đáy là trung điểm của cạnh AB, góc giữa đường thẳng SC và mặt phẳng đáy bằng 60 0 . Tính góc giữa hai đường thẳng SB và AC
A. 60 0
![]()
![]()
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a . Gọi M, N lần lượt là trung điểm của các cạnh AB, AD; H là giao điểm của CN và DM. Biết SH=a và vuông góc với mặt đáy (ABCD). Khoảng cách giữa hai đường thẳng MD và SC là
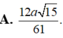
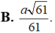
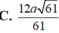
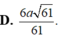
Hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a. Các cạnh bên SA = SB = SC = SD = a√2. Gọi I và K lần lượt là trung điểm của AD và BC.
a) Chứng minh mặt phẳng (SIK) vuông góc với mặt phẳng (SBC).
b) Tính khoảng cách giữa hai đường thẳng AD và SB.
Cho hình chóp S.ABCD có ABCD là hình thang cân (AD//BC) và BC = 2AD = 2a, A B C ^ = 60 ° . Gọi M, N, E lần lượt là trung điểm của AB, CD, SA. SA ⊥ (ABCD) và SA = a 2 . Khoảng cách giữa hai mặt phẳng (MNE) và (SBC) là:
A. 2 a 66 11
B. a 66 11
C. a 66 22
D. 3 a 66 22
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, AB = 2a, BC = CD = AD = a. Gọi M là trung điểm của AB. Biết SC = SD = SM và góc giữa cạnh bên SA và mặt phẳng đáy (ABCD) là 30 0 . Thể tích hình chóp đó là:
A . 3 a 3 6
B . 3 a 3 2
C . 3 3 a 3 2
D . 3 a 3 8
Cho hình chóp đều SABCD có cạnh đáy bằng a căn 2 cạnh bên bằng 2a. Gọi O là tâm của đáy , gọi lần lượt I,J là trung điểm của BC,AD.
a)Chứng minh : mp (SBC) vuông mp(SIJ)
b) Tính góc giữa đường thẳng SC và mặt phẳng (ABCD)
c) Tính khoảng cách giữa 2 đường thẳng AD và SB
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB=a, BC=a 3 Cạnh bên SA =a và vuông góc với đáy (ABCD) Cosin của góc tạo bởi giữa đường thẳng BD và mặt phẳng (SBC) bằng
A. 3 2
B. 14 4
C. 3 5
D. 22 5