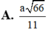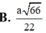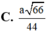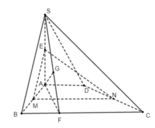
+ Ta có: M N // B C ⇒ M N // S B C E M // S B ⇒ E M // S B C ⇒ M N E // S B C
⇒ d((MNE); (SBC)) = d(M; (SBC))
+ Lại có: AM ∩ (SBC) = B ⇒ d A ; S B C d M ; S B C = A B M B = 2 ⇒ d(M; (SBC)) = 1/2 d(A;(SBC))
⇒ d ((MNE);(SBC)) = 1/2 d(A;(SBC))
+ Từ A hạ AF ⊥ BC tại F, AG ⊥ SF tại G
B C ⊥ S A B C ⊥ A F ⇒ B C ⊥ S A F ⇒ B C ⊥ A G mà AG ⊥ SF nên AG ⊥ (SBC)
⇒ d(A;(SBC)) = AG
+ Tính AG
Do ABCD là hình thang cân, BC = 2a nên suy ra BF = a/2
⇒ AF = BF. tan 60 ° = a 3 2
Tam giác SAF vuông tại A có AG là đường cao
⇒ 1 A G 2 = 1 S A 2 + 1 A F 2 ⇒ AG = a 66 11
⇒ d ((MNE);(SBC)) = 1/2 d(A;(SBC)) = 1/2 AG = a 66 22 .
Đáp án C