Chọn B
Lời giải. Để cho gọn ta chọn a=1
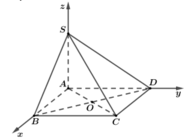
Chọn hệ trục tọa độ Oxyz như hình vẽ với A(0;0;0) và B(1;0;0) , D(0; 3 ;0)
Suy ra C(1; 3 ;0)
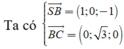
VTPT của mặt phẳng (SBC) là
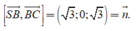
Đường thẳng có VTCP là
![]()
Khi đó
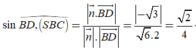
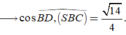
Chọn B
Lời giải. Để cho gọn ta chọn a=1

Chọn hệ trục tọa độ Oxyz như hình vẽ với A(0;0;0) và B(1;0;0) , D(0; 3 ;0)
Suy ra C(1; 3 ;0)
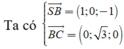
VTPT của mặt phẳng (SBC) là
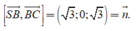
Đường thẳng có VTCP là
![]()
Khi đó
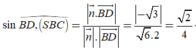
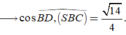
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật A B = a 3 , B C = a 2 . Cạnh bên SA=a và SA vuông góc với mặt phẳng đáy. Khoảng cách giữa SB và DC bằng:
![]()
![]()
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh bên SA vuông góc với mặt phẳng đáy, SA = AB = a. Tính góc giữa đường thẳng SC và mặt phẳng .
A. arcsin 1 4
B. arcsin 1 3
C. arcsin 1 3
D. arcsin 2 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 3a, SA = a 3 vuông góc với đáy. Góc giữa đường thẳng SD và mặt phẳng (ABCD) bằng:
![]()
![]()
![]()
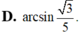
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a và SA ⊥ (ABCD).
a) Chứng minh BD ⊥ SC.
b) Chứng minh (SAB) ⊥ (SBC).
c) Cho SA = (a√6)/3. Tính góc giữa SC và mặt phẳng (ABCD).
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB=a, AD=2a, SA=3a và SA vuông góc với mặt đáy. Góc giữa đường thẳng SD và mặt phẳng (ABCD) là
A. S A D ^
B. A S D ^
C. S D A ^
D. B S D ^
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bên SA vuông góc với mặt phẳng đáy, SA = AB = a Tính góc giữa đường thẳng SC và mặt phẳng (SBD)
A. arcsin 1 4 B. arcsin 1 3 C. arcsin 1 3 D. arcsin 2 3
B. arcsin 1 3
C. arcsin 1 3
D. arcsin 2 3
Hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = 1 và AD = 3 . Cạnh bên SA vuông góc với mặt phẳng đáy và SC tạo với mặt phẳng (ABCD) một góc 60 0 . Tính thể tích V của khối chóp S,ABCD
A. V = 3
B. V = 2
C. V = 6
D. V = 1
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, AD = 2 3 . Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Gọi M, N, P lần lượt là trung điểm của các cạnh SA, CD, CB. Tính côsin góc tạo bởi mặt phẳng (MNP) và (SCD).
A. 2 435 145
B. 11 435 145
C. 2 870 145
D. 3 145 145
Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB = a, B C = a 3 . Cạnh bên SA vuông góc với đáy và đường thẳng SC tạo với mặt phẳng (SAB) một góc 30 0 . Tính thể tích V của khối chóp S.ABCD theo a.
A. 2 a 3 6 3
B. 2 a 3 3
C. 3 a 3
D. 3 a 3 3