ĐKXĐ: \(x+m\ne0\Rightarrow-m\ne\left(1,+\infty\right)\Rightarrow-m\le1\Rightarrow m\ge-1\)
\(f\left(x\right)=\dfrac{x^2+mx+1}{x+m}\)
\(f'\left(x\right)=\dfrac{\left(2x+m\right)\left(x+m\right)-x^2-mx-1}{\left(x+m\right)^2}=\dfrac{x^2+2mx+m^2-1}{\left(x+m\right)^2}\)
\(f'\left(x\right)=0\Rightarrow\left(x+m\right)^2=1\Rightarrow\left[{}\begin{matrix}x=-m+1\\x=-m-1\end{matrix}\right.\)
bbt:
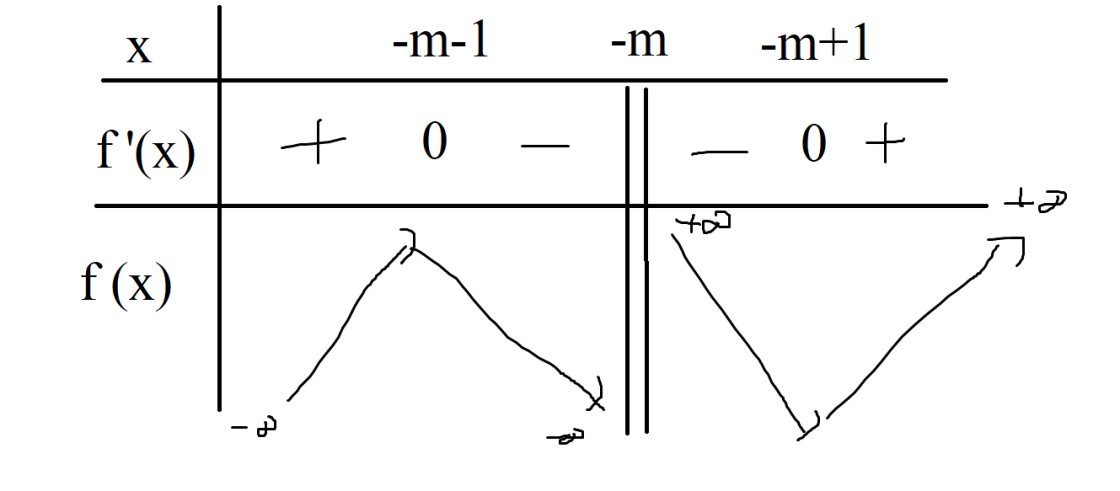
Để f(x) có giá trị nhỏ nhất trên \(\left(1,+\infty\right)\) thì \(-m+1>1\)
\(\Rightarrow-m>0\Rightarrow m< 0\Rightarrow-1\le m< 0\)
Vậy có một giá trị nguyên \(m=-1\) thỏa đề













