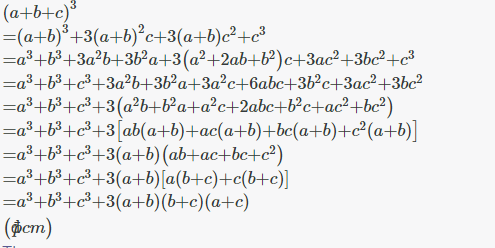\(\left(a+b+c\right)^3\\ =\left(\left(a+b\right)+c\right)^3\\ =\left(a+b\right)^3+c^3+3\left(a+b\right)c\left(a+b+c\right)\\ =a^3+b^3+3\left(a+b\right)\left(ab+c\left(a+b+c\right)\right)\\ =a^3+b^3+c^3+3\left(a+b\right)\left(b+c\right)\left(a+c\right)\)
`=>đpcm`
`(a+b+c)^3 = (a+b+c)^2(a+b+c) = (a^2 + b^2 + c^2 + 2ab + 2ac + 2bc)(a+b+c) = a^3 + 3a^2b + 6abc + 3ac^2 + b^3 + 3ab^2 + 3bc^2 + c^3 + 3ca^2 + 3cb^2`.
`= a^3 + b^3 + c^3 + 3(a+b)(b+c)(c+a)`.