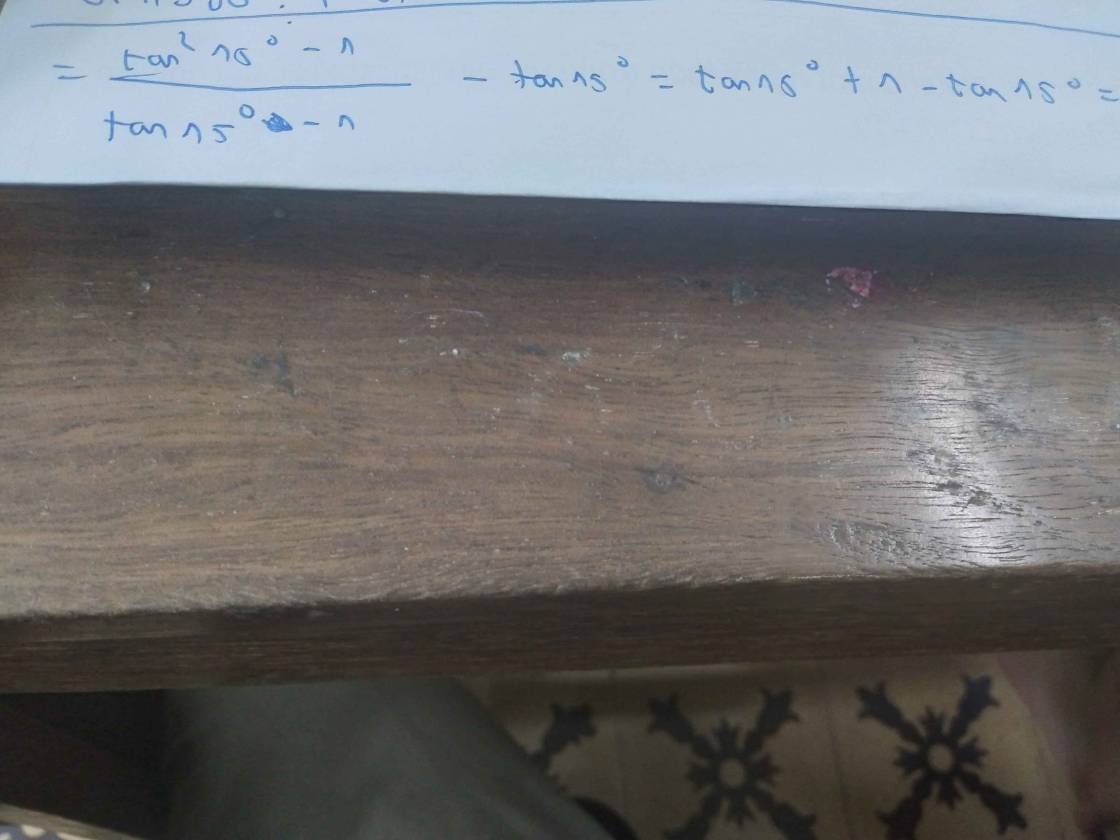Question

Chứng minh rằng \(\dfrac{tan^215^0-1}{cot75^0-1}-tan15^0=1\)

Answer 1

Ta có: `VT=[cot^2 75^o -1]/[cot 75^o -1]-cot 75^o`

               `=[(cot 75^o -1)(cot 75^o +1)]/[cot 75^o -1]-cot 75^o`

              `=cot 75^o +1-cot 75^o =1=VP`

  `=>Đpcm`

Answer 2

\(\dfrac{tan^215^o-1}{cot75^o-1}-tan15^o\)

\(=\dfrac{cot^275^o-1}{cot75^o-1}-cot75^o\)

\(=\dfrac{\left(cot75^o+1\right)\left(cot75^o-1\right)}{cot75^o-1}-cot75^o\)

\(=cot75^o+1-cot75^o\)

=1

Answer 3

 

  =1