NL: đề ở trong TCN tus mới nhìn thấy hết!
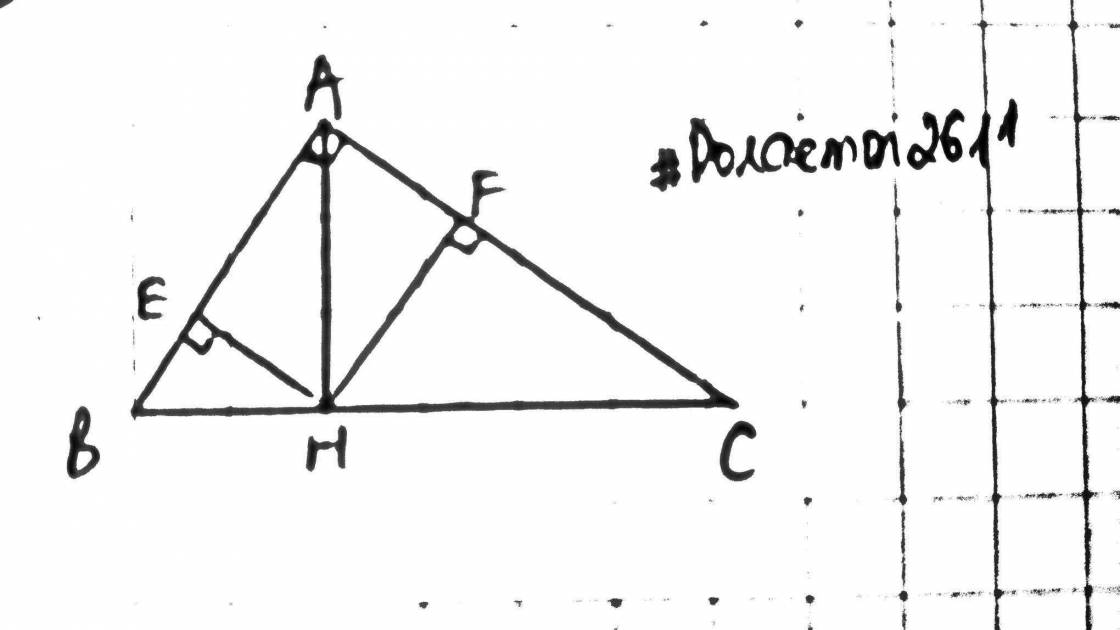
Xét `\triangle AHB` vuông tại `H` có: `HE` là đường cao
`=>AH.HB=HE.AB=>AH=[HE.AB]/[HB]` `(1)`
Xét `\triangle AHC` vuông tại `H` có: `HF` là đường cao
`=>AH.HC=HF.AC=>AH=[HF.AC]/[HC]` `(2)`
Xét `\triangle ABC` vuông tại `A` có: `AH` là đường cao
`=>AH.BC=AB.AC=>AH=[AB.AC]/[BC]` `(3)`
Từ `(1);(2);(3)=>AH^3=[HE.AB.HF.AC.AB.AC]/[HB.HC.BC]`
`=HE.HF[AB^2]/[HB].[AC^2]/[HC].1/[BC]`
`=HE.HF.BC.BC.1/[BC]=HE.HF.BC` (Đpcm)