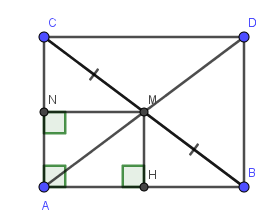
a) Do ΔABC vuông tại A (gt)
⇒ ∠BAC = 900
⇒ ∠HAN = 900
Do MN ⊥ AC (gt)
⇒ ∠ANM = 900
Do MH ⊥ AB (gt)
⇒ ∠AHM = 900
Tứ giác MHAN có:
∠HAN = ∠ANM = ∠AHM = 900
⇒ MHAN là hình chữ nhật
b) Do MA = MD (gt)
⇒ M là trung điểm của AD
Tứ giác ABDC có:
M là trung điểm của BC (gt)
M là trung điểm của AD (cmt)
⇒ ABDC là hình bình hành
Mà ∠BAC = 900
⇒ ABDC là hình chữ nhật
Cho tam giác ABC vuông tại A (AB < AC). Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a) Chứng minh tứ giác ABDC là hình chữ nhật.
b)Lấy điểm E sao cho B là trung điểm của AE. Chứng minh tứ giác BEDC là hình bình hành. c) Lấy điểm K thuộc đoạn thẳng BD sao cho KD = 2BK. CM: EK, AC, BD là đồng quy
Cho tam giác ABC vuông tại A(AB>AC). Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD=MA. a) Chứng minh tứ giác ABDC là hình chữ nhật. b) Gọi E là điểm đối xứng của C qua A. Chứng minh tứ giác ADBE là hình bình hành.
Cho tam giác ABC vuông tại A (AB > AC). Kẻ đường cao AH (H thuộc BC). Gọi M là trung điểm của AC. Trên tia đối của tia MH lấy điểm D sao cho MD = MH.
a) Chứng minh tứ giác ADCH là hình chữ nhật
b) Gọi E là điểm đối xứng của C qua H. Chứng minh tứ giác ADHE là hình bình hành
c) Vẽ EK vuông góc với AB tại K. Gọi I là trung điểm của AK. Chứng minh KE // IH
d) Gọi N là trung điểm của BE. Chứng minh HK vuông góc KN
Cho tam giác ABC vuông tại A (AB>AC). Gọi M là trung điểm của BC. Trên tia đối tia MA lấy điểm D sao cho MD=MA.
A) chứng minh tứ giác ABDC là hình chữ nhật
B) gọi E là điểm đối xứng của qua A. Chứng minh tứ giác ADBE là hình bình hành.
C) EM cắt AB tại K và cắt CD tại I. Vẽ IH vuông góc với AB(H thuộc AB). Chứng minh tam giác IKB cân
6. Cho tam giác ABC vuông tại A (AB < AC). Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a) Chứng minh tứ giác ABDC là hình chữ nhật.
b) Gọi E là điểm đối xứng của A qua B. Chứng minh tứ giác BEDC là hình bình hành.
c) EM cắt BD tại K. Chứng minh: EK = 2KM.
Cho tam giác ABC vuông tại (AB>AC). Gọi M trung điểm của BC.Trên tia đối của tia MA lấy điểm D sao cho MD=MA
a) Chứng minh tứ giác ABDC là hình chữ nhật
b) Gọi E là điểm đối xứng của C qua A .Chứng minh tứ giác ADBE là hình bình hành
c) EM cắt AB tại K và cắt CD tại I . Vẽ IH vuông góc AB .Chứng minh tam giác IKB cân
Cho tam giác ABC vuông tại A (AB<AC), đường cao AH. Gọi M là trung điểm của BC, D là điểm đối xứng với A qua M.
a) Chứng minh tứ giác ABDC là hình chữ nhật
b) Trên tia đối của tia HA lấy điểm E sao sho HA = HE. Chứng minh DB là phân giác của góc ADE.
c) Gọi I, K lần lượt là hình chiếu của E lên BD và CD. Chứng minh 3 điểm H,I,K thẳng hàng
Mọi người giúp mk với ạ!
Cho tam giác ABC vuông tại A có H là trung điểm của BC. Kẻ HM vuông góc với AB tại M, HN vuông góc với AC tại N. a) Chứng minh: Tứ giác AMHN là hình chữ nhật?
b) Trên tia đối của tia MH lấy điểm P sao cho M là trung điểm của PH. Tứ giác APBH là hình gì? Tam giác ABC cần có điều kiện gì để tứ giác APBH là hình vuông?
c) Lấy I sao cho H là trung điểm của IM. Hạ MK vuông góc BC tại K. Chứng minh: AK vuông góc KI?
Cho tam giác ABC vuông tại A (AB<AC). Lấy M là trung điểm của BC, từ M kẻ MN vuông góc với AB, MP vuông góc với AC (N thuộc AB, P thuộc AC)
a) Chứng minh tứ giác ANMP là hình chữ nhật
b) Gọi E là trung điểm của MP. Chứng minh E là trung điểm của NC
c)Đường thẳng đi qua C và song song với AM cắt MP tại G. Gọi K là giao điểm của tia GA với tia MN. Chứng minh A là trung điểm của GK.
d) Kẻ AH vuông góc với BC. Gọi O là giao điểm của AM và NP. Tam giác ABC cần có thêm điều kiện gì để HO//AB
giúp mik với
mai mình nộp rồi
Cho tam giác ABC vuông tại A . M là trung điểm của BC . Trên tia đối của MA lấy điểm D sao cho MD=MA
a) Chứng minh tứ giác ABCD là hình chữ nhật
b) Từ A kẻ AH vuông góc với BC( H thuộc BC). Gọi I,K theo thứ tự là chân đường vuông góc hạ từ H đến AB và AC. Chứng minh rằng AH=IK
b) Chứng minh IK vuông góc với AM
