Cho tam giác ABC vuông tại A (AB < AC). Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a) Chứng minh tứ giác ABDC là hình chữ nhật.
b)Lấy điểm E sao cho B là trung điểm của AE. Chứng minh tứ giác BEDC là hình bình hành. c) Lấy điểm K thuộc đoạn thẳng BD sao cho KD = 2BK. CM: EK, AC, BD là đồng quy
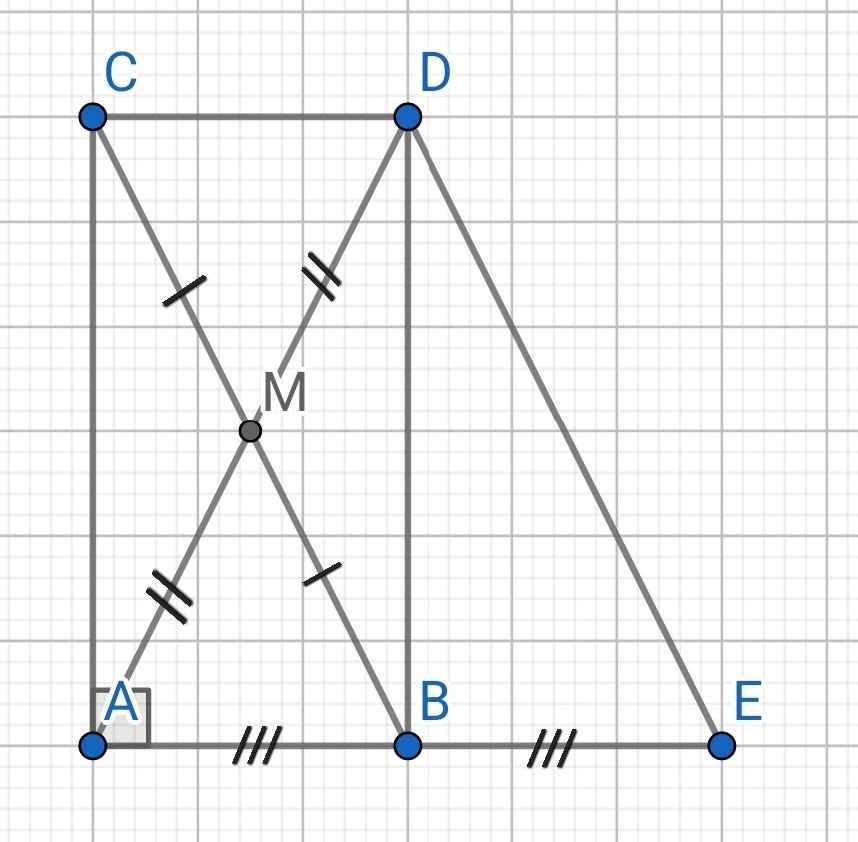a) Tứ giác ABDC có:
M là trung điểm của BC (gt)
M là trung điểm của AD (gt)
⇒ ABDC là hình bình hành
Mà ∠BAC = 90⁰ (∆ABC vuông tại A)
⇒ ABDC là hình chữ nhật
b) Do ABDC là hình chữ nhật (cmt)
⇒ CD = AB (1)
Do B là trung điểm của AE (gt)
⇒ BE = AB = AE : 2 (2)
Từ (1) và (2) ⇒ CD = BE
Do ABDC là hình chữ nhật (cmt)
⇒ CD // AB
⇒ CD // BE
Tứ giác BEDC có:
CD // BE (cmt)
CD = BE (cmt)
⇒ BEDC là hình bình hành
c) Do ABDC là hình chữ nhật (cmt)
⇒ AC // BD
Do đó AC, BD, EK đồng quy là vô lý
Em xem lại đề nhé!
ABC vuông tại A (AB < AC), trung tuyến AM, đường cao AH. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
AB tại E, HF 
