Câu này ko nên đạo hàm ngay lập tức mà nên làm đơn giản bài toán đi trước khi sử dụng đạo hàm
Nhận thấy \(x=0\) ko phải nghiệm, chia 2 vế cho \(x^2\)
\(\Rightarrow x^2+mx-2\left(m^2-1\right)+\dfrac{m}{x}+\dfrac{1}{x^2}=0\)
\(\Leftrightarrow\left(x+\dfrac{1}{x}\right)^2+m\left(x+\dfrac{1}{x}\right)-2m^2=0\)
Đặt \(x+\dfrac{1}{x}=t\Rightarrow\left[{}\begin{matrix}t\ge2\\t\le-2\end{matrix}\right.\)
\(\Rightarrow f\left(t\right)=t^2+mt-2m^2=0\) (1)
Pt đã cho có đúng 4 nghiệm pb khi (1) có 2 nghiệm pb thỏa mãn: \(\left[{}\begin{matrix}t>2\\t< -2\end{matrix}\right.\)
\(f'\left(t\right)=2t+m=0\Rightarrow t=-\dfrac{m}{2}\) ; \(f\left(-\dfrac{m}{2}\right)=-\dfrac{9m^2}{4}\)
\(f\left(-2\right)=-2m^2-2m+4\) ; \(f\left(2\right)=-2m^2+2m+4\)
Có 3 TH xảy ra:
TH1: \(-\dfrac{m}{2}< -2\Rightarrow m>4\)
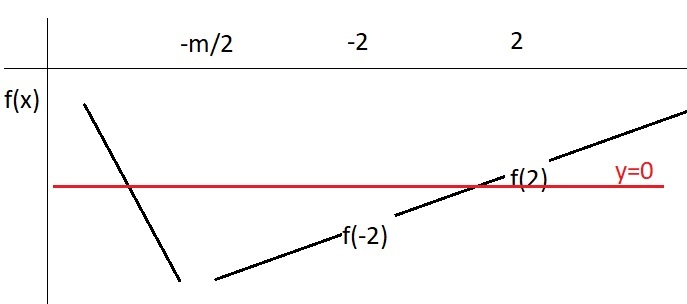
Từ BBT \(\Rightarrow\left[{}\begin{matrix}f\left(2\right)< 0\\-\dfrac{9m^2}{4}< 0< f\left(-2\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}-2m^2+2m+4< 0\\\left\{{}\begin{matrix}m\ne0\\-2m^2-2m+4>0\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}m< -1\\m>2\end{matrix}\right.\\\left\{{}\begin{matrix}m\ne0\\-2< m< 1\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow m>4\)
TH2: \(-\dfrac{m}{2}>2\Rightarrow m< -4\)
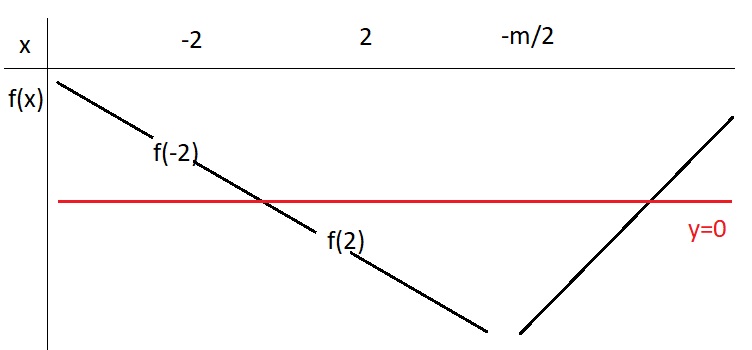
Từ BBT \(\Rightarrow\left[{}\begin{matrix}f\left(-2\right)< 0\\-\dfrac{9m^2}{4}< 0< f\left(2\right)\end{matrix}\right.\) \(\Rightarrow m< -4\)
TH3: \(-2\le-\dfrac{m}{2}\le2\Rightarrow-4\le m\le4\)
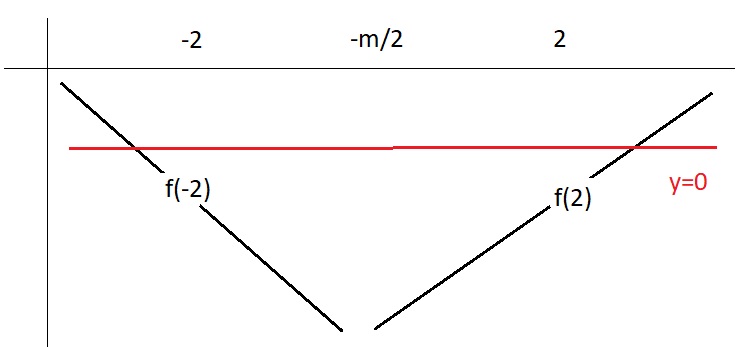
Từ BBT \(\Rightarrow\left[{}\begin{matrix}0>f\left(2\right)\ge f\left(-2\right)\\0>f\left(-2\right)\ge f\left(2\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}0>-2m^2+2m+4\ge-2m^2-2m+4\\0>-2m^2-2m+4\ge-2m^2+2m+4\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m>2\\m< -2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}-4\le m< -2\\2< m\le4\end{matrix}\right.\)
Kết hợp lại \(\Rightarrow\left[{}\begin{matrix}m>2\\m< -2\end{matrix}\right.\)















