Question

Cho hình lăng trụ ABC.A'B'C' có đáy là tam giác vuông cân tại A, AB \(=a\sqrt{3}\), AA'= A'B = A'C = 2a. Tính số đo góc nhị diện [A,BC, C']

Answer 1

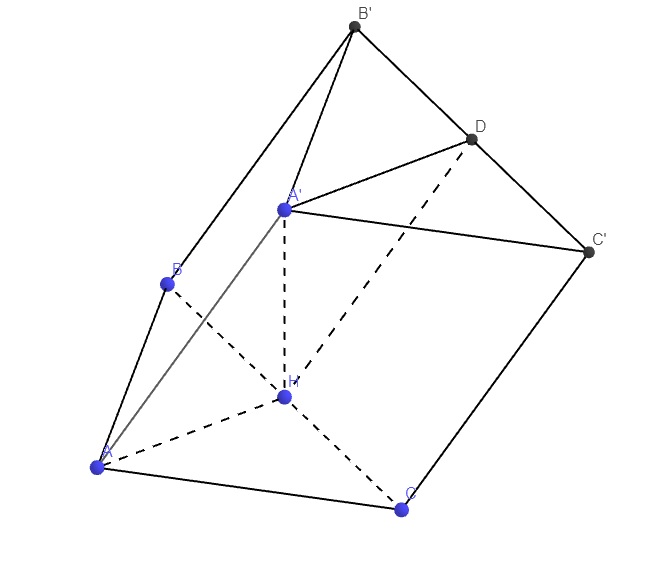
Gọi H là trung điểm BC thì H đồng thời là tâm đường tròn ngoại tiếp đáy

Do \(A'A=A'B=A'C\) nên hình chiếu của A' lên (ABC) trùng tâm đường tròn ngoại tiếp (ABC)

\(\Rightarrow A'H\perp\left(ABC\right)\)

Gọi D là trung điểm B'C' \(\Rightarrow BC\perp\left(A'AHD\right)\) nên \(\widehat{DHA}\) là góc cần tìm

\(BC=AB\sqrt{2}=a\sqrt{6}\); \(AH=A'D=\dfrac{BC}{2}=\dfrac{a\sqrt{6}}{2}\)

\(A'H=\sqrt{A'A^2-AH^2}=\dfrac{a\sqrt{10}}{2}\)

\(tan\widehat{A'HD}=\dfrac{A'D}{A'H}=\dfrac{\sqrt{15}}{5}\) \(\Rightarrow\widehat{A'HD}=37^045'\)

\(\Rightarrow\widehat{DHA}=90^0+\widehat{A'HD}=127^045'\)

Tính nhầm chỗ nào ko mà kết quả ko đẹp

Answer 2

Answer 3