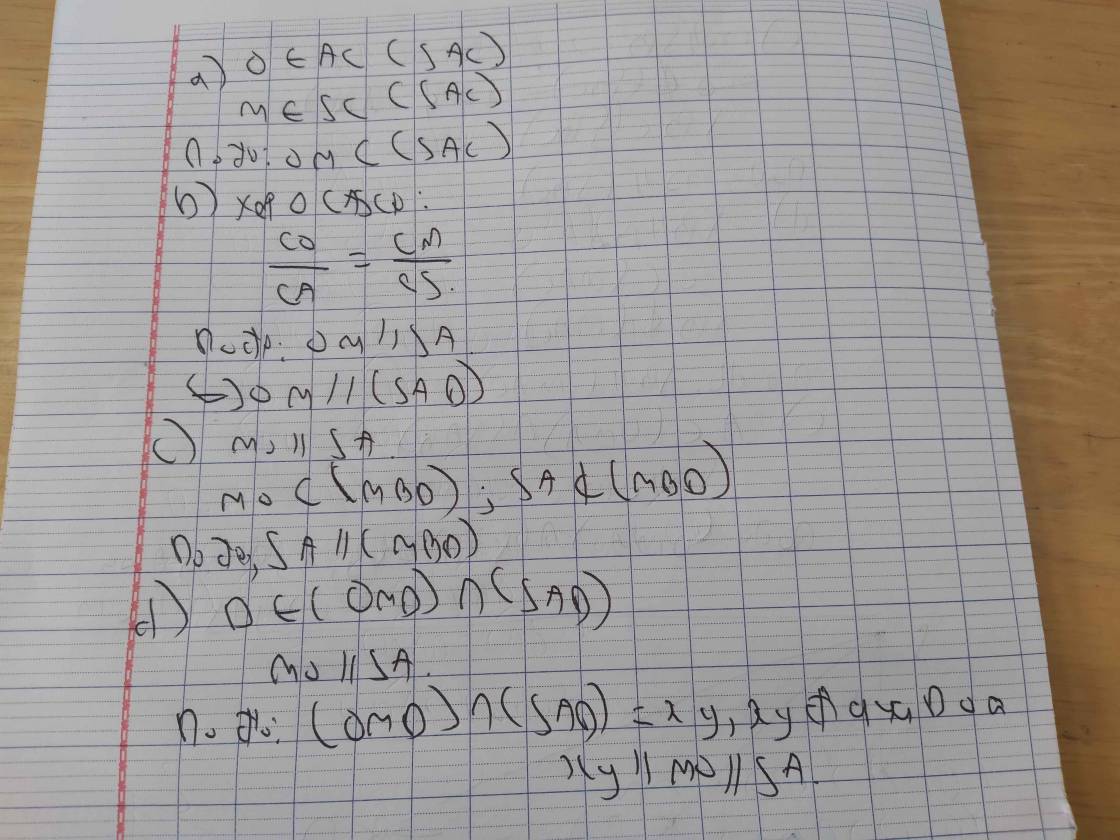Các câu hỏi tương tự
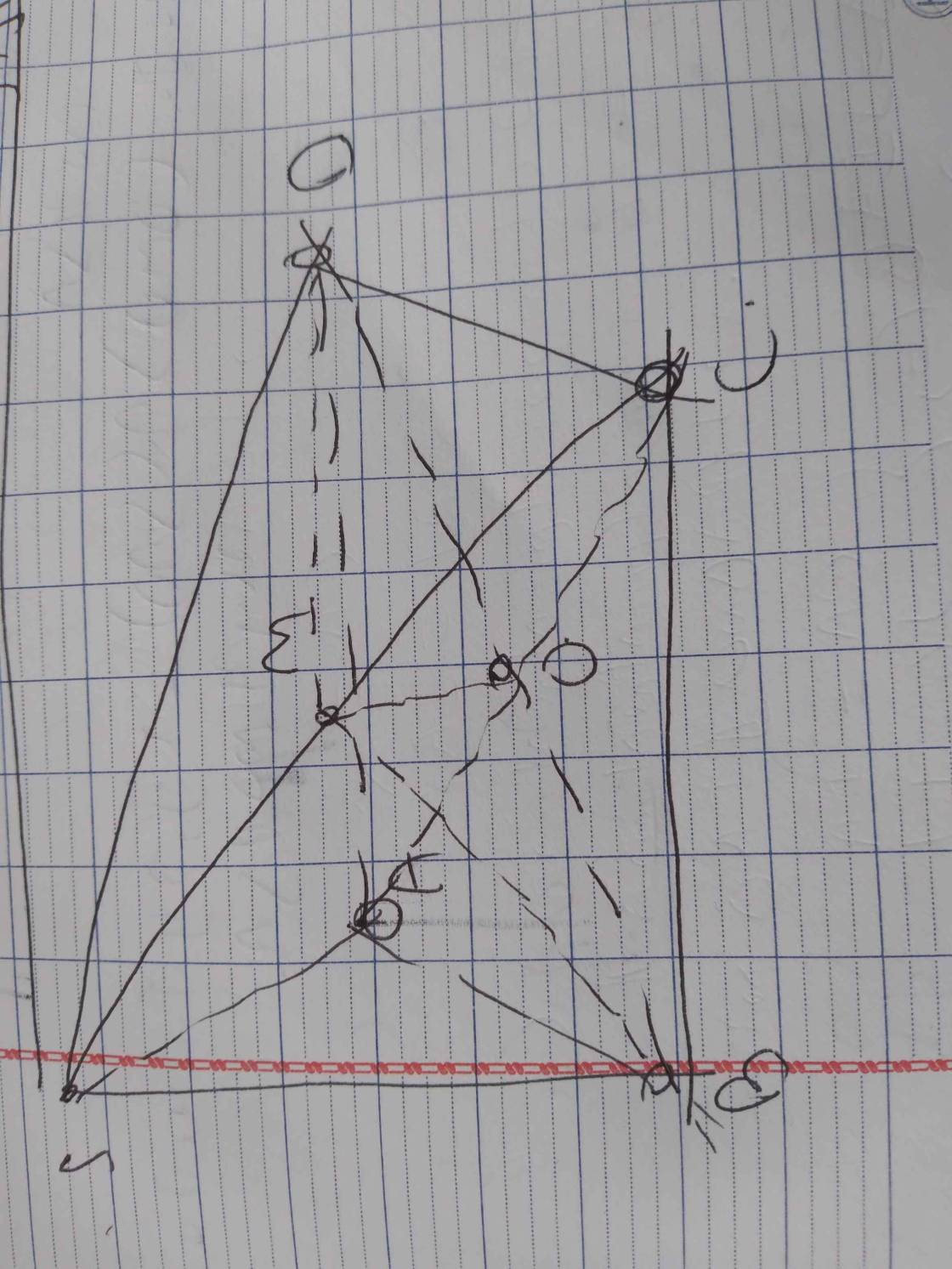
cho hình chóp S.ABCD, đáy ABCD là hình bình hành, tâm O. Gọi M là trung điểm SC
a) vẽ hình
b) xét vị trí tương đối của OM và (SAC)
c) chứng minh OM ∥ (SAD)
d) chứng minh SA ∥ (MBD)
e) tìm giao tuyến của (OMD) và (SAD)
cho hình chóp S.ABCD, đáy ABCD là hình bình hành, tâm O. Gọi M là trung điểm SC
a) vẽ hình
b) xét vị trí tương đối của OM và (SAC)
c) chứng minh OM ∥ (SAD)
d) chứng minh SA ∥ (MBD)
e) tìm giao tuyến của (OMD) và (SAD)
cho hình chóp S.ABCD, đáy ABCD là hình bình hành, tâm O. Gọi M là trung điểm SC
a) vẽ hình
b) xét vị trí tương đối của OM và (SAC)
c) chứng minh OM ∥ (SAD)
d) chứng minh SA ∥ (MBD)
e) tìm giao tuyến của (OMD) và (SAD)
cho hình chóp S.ABCD đáy ABCD là hình bình hành, tâm O. Gọi M là trung điểm SD
a) xác định vị trí tương đối của OM và (SBD)
b) Chứng minh OM ll (SBA)
c) Chứng minh OM ll (SBC)
d) Chứng minh SB ll (MAC)
e) tìm giao tuyến (OMA) và (SAB)
cho hình chóp S.ABCD đáy ABCD là hình bình hành tâm O. Gọi M là trung điểm SC
a) chứng minh SA // (MBD)
b) tìm giao tuyến của (OMD) và (SAD)
cho hình chóp S.ABCD, đáy ABCD là hình bình hành, tâm O. Gọi M là trung điểm SD
a) vẽ hình
b) xét vị trí tương đối của OM và (SBD)
c) chứng minh OM ∥ (SBA)
d) chứng minh OM ∥ (SBC)
e) chứng minh SB ∥ (MAC)
f) tìm giao tuyến của (OMA) và (SAB)
Cho hình chóp S.ABCD có đáy là hình bình hành, tâm O. Gọi M, N lần lượt là trung điểm của AB, CD.
1. Xác định giao tuyến của (SBC) và (SAD).
2. Chứng minh MN // (SBC); MN // (SAD).
3. Gọi I là trung điểm của SA. Tìm giao điểm K của (INM) và SD.
4. Chứng minh SB, SC // (IMN).
5. Gọi H là trung điểm của IO. Chứng minh HK // (SBC).
giải giúp mình với
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O và M là trung điểm của SD.
a, tìm giao tuyến của hai mặt phẳng (SAC) và (SBD).
b, chứng minh rằng MO song song với mặt phẳng (SAD).
cho hình chóp S.ABCD đáy ABCD là hình bình hành tâm O. Gọi M là trung điểm SC
a) chứng minh SB // (MAC)
b) tìm giao tuyến của (OMA) và (SAB)