Question

Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, SC ⊥ (ABCD) và SC=3a. Tính góc phẳng nhị diện [B, SA, C]

Answer 1

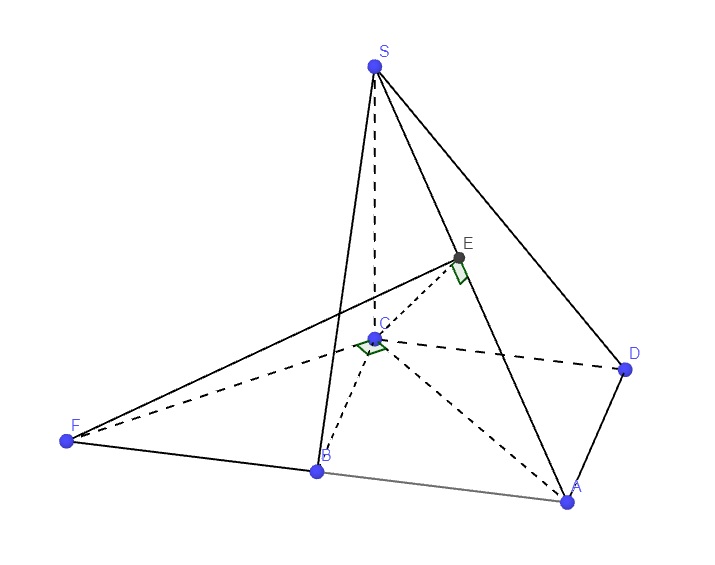
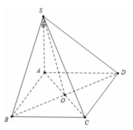
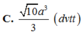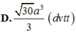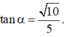Trong mp (SAC), từ A kẻ \(CE\perp SA\) (1)

Trong mp (ABCD), qua C kẻ đường thẳng vuông góc AC cắt AB kéo dài tại F

\(\Rightarrow FC\perp AC\)

Do \(SC\perp\left(ABCD\right)\Rightarrow SC\perp FC\)

\(\Rightarrow FC\perp\left(SAC\right)\Rightarrow FC\perp SA\) (2)

(1);(2) \(\Rightarrow SA\perp\left(FEC\right)\)

\(\Rightarrow\left[B,SA,C\right]=\widehat{FEC}\)

\(AC=AB\sqrt{2}=2a\sqrt{2}\)

Hệ thức lượng: \(CE=\dfrac{SC.AC}{\sqrt{SC^2+AC^2}}=\dfrac{6a\sqrt{34}}{17}\)

\(FC=AC.tan45^0=2a\sqrt{2}\)

\(\Rightarrow tan\widehat{FEC}=\dfrac{FC}{EC}=\dfrac{\sqrt{17}}{3}\Rightarrow\widehat{FEC}\approx54^0\)

Answer 2