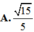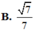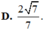a: AC vuông góc SB
AC vuông góc BC
=>AC vuông (SBC)
b: BH vuông góc SC
BH vuông góc AC
=>BH vuông góc (SAC)
=>BH vuông góc SA
c: (SA;ABC)=(AS;SB)=góc ASB
\(BA=\sqrt{CB^2+CA^2}=a\sqrt{3}\)
\(SA=\sqrt{SB^2+BA^2}=a\sqrt{7}\)
sin ASB=AB/SA=căn 3/căn 7
=>góc ASB=41 độ
(SA;(SBC))=(SA;SC)=góc ASC
\(SC=\sqrt{\left(2a\right)^2+a^2}=a\sqrt{5}\)
Vì SC^2+CA^2=SA^2
nên ΔSAC vuông tại C
=>sin ASC=AC/SA=căn 2/căn 7
=>góc ASC=32 độ