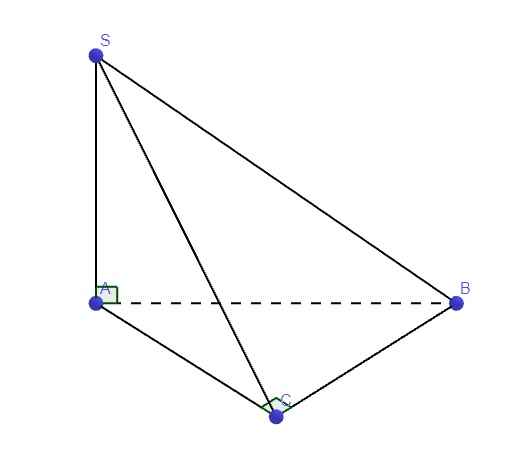
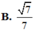\(SA\perp\left(ABC\right)\Rightarrow AB\) là hình chiếu vuông góc của SB lên (ABC)
\(\Rightarrow\widehat{SBA}\) là góc giữa SB và (ABC)
\(AB=AC\sqrt{2}=a\sqrt{2}\)
\(tan\widehat{SBA}=\dfrac{SA}{AB}=\sqrt{\dfrac{3}{2}}\Rightarrow\widehat{SBA}\approx50^046'\)
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AC\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAC\right)\)
\(\Rightarrow SC\) là hình chiếu vuông góc của SB lên (SAC)
\(\Rightarrow\widehat{BSC}\) là góc giữa SB và (SAC)
\(SB=\sqrt{SA^2+AB^2}=a\sqrt{5}\) ; \(BC=AC=a\)
\(sin\widehat{BSC}=\dfrac{BC}{SB}=\dfrac{1}{\sqrt{5}}\Rightarrow\widehat{BSC}\approx26^034'\)
b.
Theo cmt, \(BC\perp\left(SAC\right)\)
Mà \(BC=\left(SBC\right)\cap\left(ABC\right)\)
\(\Rightarrow\widehat{SCA}\) là góc giữa (SBC) và (ABC)
\(tan\widehat{SCA}=\dfrac{SA}{AC}=\sqrt{3}\Rightarrow\widehat{SCA}=60^0\)
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\\SA\in\left(SAC\right)\end{matrix}\right.\) \(\Rightarrow\left(SAC\right)\perp\left(ABC\right)\)
\(\Rightarrow\) Góc giữa (SAC) và (ABC) là 90 độ