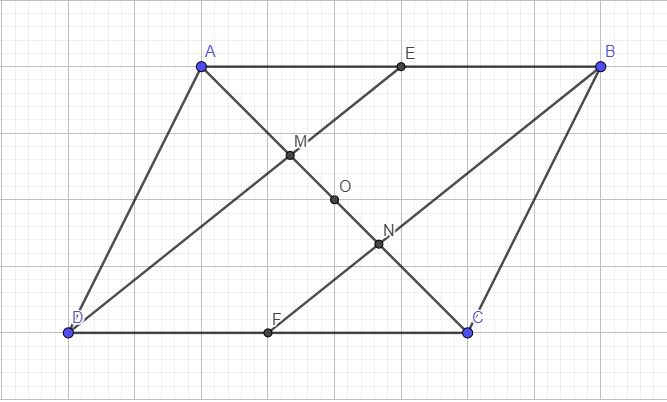
Bổ sung đề: AC cắt BD tại O
Ta có: \(AE=EB=\dfrac{AB}{2}\)
\(CF=FD=\dfrac{CD}{2}\)
mà AB=CD
nên AE=EB=CF=FD
Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
Xét tứ giác BEDF có
BE//DF
BE=DF
Do đó: BEDF là hình bình hành
=>DE//BF
Ta có: BEDF là hình bình hành
=>BD cắt EF tại trung điểm của mỗi đường
=>O là trung điểm của EF
Xét ΔANB có
E là trung điểm của AB
EM//BN
Do đó: M là trung điểm của AN
=>AM=MN
Xét ΔDMC có
F là trung điểm của CD
FN//DM
Do đó: N là trung điểm của CM
=>CN=NM
=>AM=MN=CN
Xét ΔMAE và ΔNCF có
MA=NC
\(\widehat{MAE}=\widehat{NCF}\)
AE=CF
Do đó: ΔMAE=ΔNCF
=>ME=NF
Xét tứ giác MENF có
ME//NF
ME=NF
Do đó: MENF là hình bình hành
=>MN cắt EF tại trung điểm của mỗi đường
mà O là trung điểm của EF
nên O là trung điểm của MN
=>M đối xứng N qua O
Do \(\left\{{}\begin{matrix}EB=\dfrac{1}{2}AB\\DF=\dfrac{1}{2}CD\\AB=CD\end{matrix}\right.\) \(\Rightarrow EB=DF\)
Mà \(AB||CD\Rightarrow EB||DF\)
\(\Rightarrow EBFD\) là hình bình hành (tứ giác có cặp cạnh đối song song và bằng nhau)
\(\Rightarrow\widehat{EBF}=\widehat{EDF}\)
Lại có ABCD là hình bình hành \(\Rightarrow\widehat{B}=\widehat{D}\)
\(\Rightarrow\widehat{B}-\widehat{EBF}=\widehat{D}-\widehat{EDF}\Rightarrow\widehat{CBN}=\widehat{ADM}\)
Xét hai tam giác CBN và ADM có:
\(\left\{{}\begin{matrix}\widehat{CBN}=\widehat{ADM}\left(cmt\right)\\CB=AD\left(ABCD\text{ là hbh}\right)\\\widehat{BCN}=\widehat{DAM}\left(\text{so le trong}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta CBN=\Delta ADM\left(g.c.g\right)\Rightarrow CN=AM\)
Lại có O là trung điểm AC (t/c hình bình hành) \(\Rightarrow OA=OC\Rightarrow OA-AM=OC-CN\)
\(\Rightarrow OM=ON\Rightarrow M,N\) đối xứng qua O