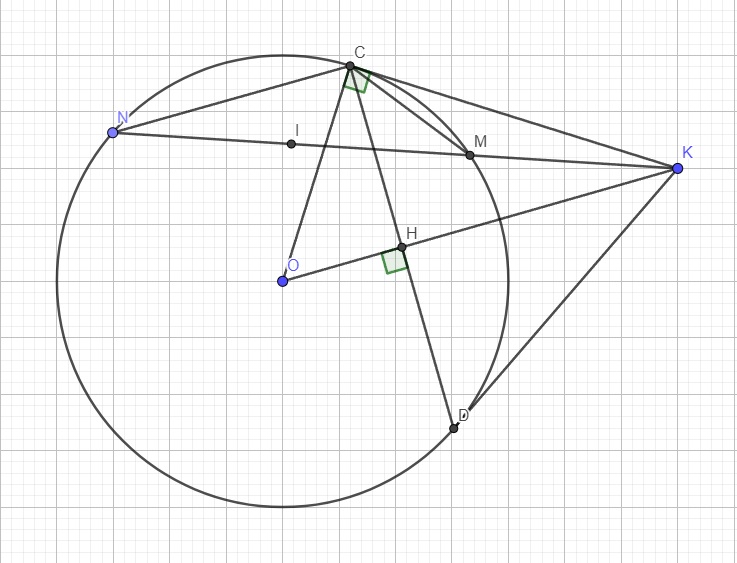
a: Xét (O) có
\(\widehat{KDM}\) là góc tạo bởi tiếp tuyến DK và dây cung DM
\(\widehat{MND}\) là góc nội tiếp chắn cung MD
Do đó: \(\widehat{KDM}=\widehat{MND}=\widehat{KND}\)
Xét ΔKDM và ΔKND có
\(\widehat{KDM}=\widehat{KND}\)
\(\widehat{DKM}\) chung
Do đó: ΔKDM~ΔKND
=>\(\dfrac{KD}{KN}=\dfrac{KM}{KD}\)
=>\(KD^2=KM\cdot KN\)
b: Xét (O) có
KC,KD là các tiếp tuyến
Do đó: KC=KD
=>K nằm trên đường trung trực của CD(1)
Ta có: OC=OD
=>O nằm trên đường trung trực của CD(2)
Từ (1) và (2) suy ra OK là đường trung trực của CD
=>OK\(\perp\)CD tại H và H là trung điểm của CD
Xét ΔKDO vuông tại D có DH là đường cao
nên \(KH\cdot KO=KD^2\)
=>\(KH\cdot KO=KM\cdot KN\)
c: Ta có: ΔOMN cân tại O
mà OI là đường trung tuyến
nên OI\(\perp\)MN
a.
Do K là giao điểm 2 tiếp tuyến tại C và D \(\Rightarrow KC=KD\) (1)
Xét hai tam giác KCM và KNC có:
\(\left\{{}\begin{matrix}\widehat{KCM}=\widehat{KNC}\left(\text{cùng chắn CM}\right)\\\widehat{CKM}\text{ chung}\end{matrix}\right.\)
\(\Rightarrow\Delta KCM\sim\Delta KNC\left(g.g\right)\)
\(\Rightarrow\dfrac{KC}{KN}=\dfrac{KM}{KC}\Rightarrow KC^2=KM.KN\) (2)
(1);(2) \(\Rightarrow KD^2=KM.KN\)
b.
\(\left\{{}\begin{matrix}OC=OD=R\\KC=KD\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow\) OK là trung trực của CD
\(\Rightarrow OK\) vuông góc CD tại H
Do KC là tiếp tuyến \(\Rightarrow KC\perp OC\)
Áp dụng hệ thức lượng trong tam giác vuông OCK với đường cao CH:
\(KC^2=KH.KO\) (3)
(2);(3) \(\Rightarrow KM.KN=KH.KO\)
c.
Do I là trung điểm MN \(\Rightarrow OI\perp MN\) (đường kính đi qua trung điểm của dây cung thì vuông góc với dây cung ấy)